题目内容
求函数y=sin（2x-
）+2，x∈R的周期、单调区间、最小值以及取得最小值的x的集合．
解：函数y=sin（2x-）+2，x∈R，周期T=
=π，
因为：2x-∈[
]k∈z
所以：函数y=sin（2x-）+2的单调增区间：[
]，k∈z
因为：2x-∈[
]k∈z
所以：函数y=sin（2x-）+2的单调减区间：[
]，k∈z
最小值1，2x-=
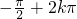，此时x∈{x|x=
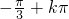，k∈z}
分析：直接利用正弦函数的正确、单调区间、最小值以及取得最小值的x的集合的求法求解即可．
点评：本题考查三角函数的基本性质，函数的单调性，周期性，最值的求法，考查学生分析问题解决问题的能力，是常考题目．
）+2，x∈R，周期T==π，因为：2x-
∈[]k∈z所以：函数y=sin（2x-
）+2的单调增区间：[]，k∈z因为：2x-
∈[]k∈z所以：函数y=sin（2x-
）+2的单调减区间：[]，k∈z最小值1，2x-
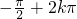=，此时x∈{x|x=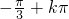，k∈z}分析：直接利用正弦函数的正确、单调区间、最小值以及取得最小值的x的集合的求法求解即可．
点评：本题考查三角函数的基本性质，函数的单调性，周期性，最值的求法，考查学生分析问题解决问题的能力，是常考题目．
练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
