题目内容
在矩形ABCD中，AB=4，BC=3，沿北将矩形ABCD折成直二面角B-AC-D，则四面体ABCD的外接球的体积为( )A.
B. 
C. 
D. 
C
解析：本题考查学生空间想象能力以及等价转化能力．关键是找到四面体ABCD的外接球的球心与半径．
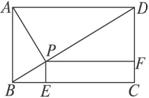
如图，注意到折叠后△ADC仍为直角三角形，取AC的中点O，则OA=OB=OC=OD= ，故点O为四面体ABCD的外接球的球心，其半径r=,代入球的体积公式可得．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=3
如图，在矩形ABCD中，已知AD=2，AB=a（a＞2），E、F、G、H分别是边AD、AB、BC、CD上的点，若AE=AF=CG=CH，问AE取何值时，四边形EFGH的面积最大？并求最大的面积．
的取值范围．
|=
.设
=a, 
=b, 
=c,求|a+b+c|.