Question

已知三点N(0,-2-a),P(t,-2-a),F(0,a)(其中a为大于零的常数,t为参数),平面内动点M满足=0,且||=||+2.

(1)求动点M的轨迹方程;

(2)若动点M的轨迹在y轴左侧部分与圆心在C(0,a+4)且半径为4的圆相交于两点S、T,求证:C落在以S、T为焦点且过F的椭圆上.

Answer 1

答案：(1)解:依题意,P点在直线y=-2-a上,又MP⊥NP,=2,

∴动点M到定直线y=-2-a的距离比它到定点F(0,a)的距离大2.

∴动点M到定直线y=-a的距离与它到定点F(0,a)的距离相等.

∴动点M的轨迹为抛物线,其方程为x²=4ay(a＞0).

(2)证明:设T(x_T,y_T),S(x_S,y_S),则由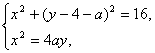得y²+2(a-4)y+a²+8a=0,

∴y_S+y_T=8-2a.又S、T在抛物线上,由抛物线的定义,得|TF|=y_T+a,|SF|=y_S+a,

∴|TF|+|SF|=y_S+y_T+2a=8.∴F在以S、T为焦点的椭圆上.

而S、T又落在圆C上,∴|SC|+|TC|=2r=8.

∴C到S、T的距离之和为定值8,即C落在以S、T为焦点过F的椭圆上.