题目内容
函数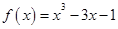
，若对于区间[－3,2]上的任意x1，x2，都有 | f(x1)－f (x2)|≤ t，则实数t的最小值是( )
| A．20 | B．18 | C．3 | D．0 |
A
解析试题分析：
所以
在区间
，
单调递增，在区间
单调递减．
，
，
，
，可知
的最大值为20 .故
的最小值为20.
考点：利用导数求函数的单调性与最值.
练习册系列答案
名校课堂系列答案
相关题目
若曲线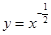
在点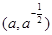
处的切线与两坐标轴围成的三角形面积为18.则
( )
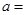| A．64 | B．32 | C．16 | D．8 |
函数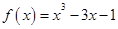
，若对于区间[－3,2]上的任意x1，x2，都有|f(x1)－f(x2)|≤t，则实数t的最小值是( )
| A．20 | B．18 | C．3 | D．0 |
定义域为R的函数f(x)满足f(1)＝1，且f(x)的导函数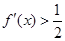
，则满足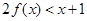
的x的集合为( )
| A．{x|x<1} | B．{x|－1<x<1} | C．{x|x<－1或x>1} | D．{x|x>1} |
设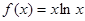
，若
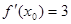，则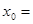
（ ）
A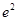． | B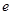． | C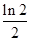． | D． |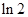
函数
的定义域为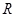
，
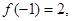对任意
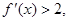则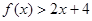
的解集为
A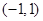． | B．（ ，+ ） |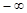
C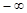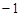．（， ） | D．（，+） |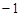
直线
在第一象限内围成的封闭图形的面积为（ ）
A． | B． | C． | D．4 |
，g(x)＝xα在点P(1,1)处的切线分别为l1，l2，且l1⊥l2，则实数α的值为( )
函数
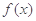是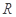
上的可导函数,
时，
，则函数
的零点个数为（ ）
A． | B． | C． | D． |