题目内容
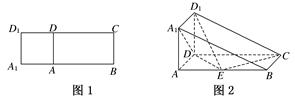
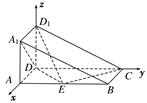
如图1,A,D分别是矩形A1BCD1上的点,AB=2AA1=2AD=2,DC=2DD1,把四边形A1ADD1沿AD折叠,使其与平面ABCD垂直,如图2所示,连接A1B,D1C得几何体ABA1DCD1.
(1)当点E在棱AB上移动时,证明:D1E⊥A1D;
(2)在棱AB上是否存在点E,使二面角D1ECD的平面角为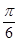 ?若存在,求出AE的长;若不存在,请说明理由.
?若存在,求出AE的长;若不存在,请说明理由.

(1)当点E在棱AB上移动时,证明:D1E⊥A1D;
(2)在棱AB上是否存在点E,使二面角D1ECD的平面角为
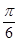 ?若存在,求出AE的长;若不存在,请说明理由.
?若存在,求出AE的长;若不存在,请说明理由.(1)见解析 (2)存在,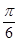
解:(1)证明,如图,以点D为坐标原点,DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系Dxyz,
则D(0,0,0),A(1,0,0),C(0,2,0),A1(1,0,1),D1(0,0,1).设E(1,t,0),
则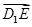 =(1,t,-1),
=(1,t,-1),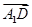 =(-1,0,-1),
=(-1,0,-1),
∴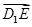 ·
·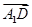 =1×(-1)+t×0+(-1)×(-1)=0,
=1×(-1)+t×0+(-1)×(-1)=0,
∴D1E⊥A1D.
(2)假设存在符合条件的点E.设平面D1EC的法向量为n=(x,y,z),
由(1)知 =(-1,2-t,0),
=(-1,2-t,0),
则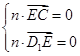 得
得
令y=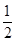 ,则x=1-
,则x=1-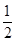 t,z=1,
t,z=1,
∴n=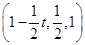 是平面D1EC的一个法向量,
是平面D1EC的一个法向量,
显然平面ECD的一个法向量为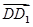 =(0,0,1),
=(0,0,1),
则cos〈n,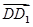 〉=
〉=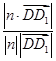
=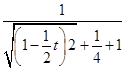 =cos
=cos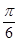 ,
,
解得t=2-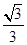 (0≤t≤2).
(0≤t≤2).
故存在点E,
当AE=2-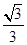 时,二面角D1ECD的平面角为
时,二面角D1ECD的平面角为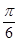 .
.

则D(0,0,0),A(1,0,0),C(0,2,0),A1(1,0,1),D1(0,0,1).设E(1,t,0),
则
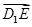 =(1,t,-1),
=(1,t,-1),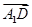 =(-1,0,-1),
=(-1,0,-1),∴
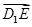 ·
·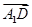 =1×(-1)+t×0+(-1)×(-1)=0,
=1×(-1)+t×0+(-1)×(-1)=0,∴D1E⊥A1D.
(2)假设存在符合条件的点E.设平面D1EC的法向量为n=(x,y,z),
由(1)知
 =(-1,2-t,0),
=(-1,2-t,0),则
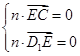 得
得
令y=
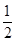 ,则x=1-
,则x=1-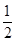 t,z=1,
t,z=1,∴n=
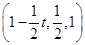 是平面D1EC的一个法向量,
是平面D1EC的一个法向量,显然平面ECD的一个法向量为
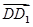 =(0,0,1),
=(0,0,1),则cos〈n,
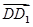 〉=
〉=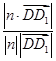
=
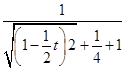 =cos
=cos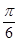 ,
,解得t=2-
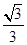 (0≤t≤2).
(0≤t≤2).故存在点E,
当AE=2-
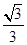 时,二面角D1ECD的平面角为
时,二面角D1ECD的平面角为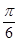 .
.
练习册系列答案
相关题目
 AB.
AB.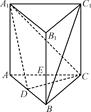
 为矩形,
为矩形, ,
,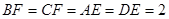 ,
,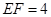 ,
, ,
,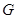 为
为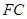 的中点,
的中点,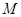 为线段
为线段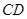 上的一点,且
上的一点,且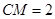 .
.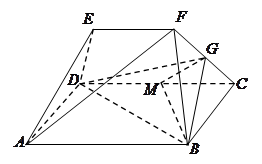
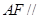 面
面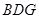 ;
;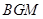
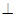 面
面 ;
; 的体积
的体积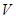 .
.
 的值.
的值. ,底面
,底面 中
中 ,棱
,棱 ,
, 分别为
分别为 的中点.
的中点.
 >的值;
>的值;

 +
+
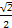
 +
+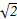





 ,且
,且 //(
//( ),则k=______.
),则k=______.