题目内容
(本小题满分10分)
直线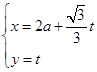 (
(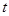 为参数,
为参数,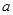 为常数且
为常数且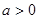 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为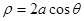 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.
弦长 .
.
解析试题分析:直线的普通方程为: ,
,
圆的普通方程为: ,
,
圆心到直线的距离 , ∴ 弦长
, ∴ 弦长 .
.
考点:本题主要考查极坐标方程与普通方程的互化,直线与圆的位置关系,点到直线的距离公式。
点评:中档题,学习参数方程、极坐标,其中一项基本的要求是几种不同形式方程的互化,其次是应用极坐标、参数方程,简化解题过程。本题将极坐标方程化为圆的标准方程,利用圆中的“特征三角形”,求得了弦长。

练习册系列答案
相关题目
如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( ).
| A.a1>a2 | B.a1<a2 |
| C.a1=a2 | D.a1,a2的大小与m的值有关 |
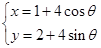 (
( 为参数),直线
为参数),直线 经过定点P(3,5),倾斜角为
经过定点P(3,5),倾斜角为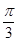 (1)写出直线
(1)写出直线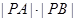 的值
的值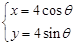 (
(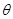 为参数),直线l经过点P(2,2),倾斜角
为参数),直线l经过点P(2,2),倾斜角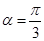 。(1)写出圆的标准方程和直线l的参数方程;
。(1)写出圆的标准方程和直线l的参数方程;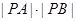 的值。
的值。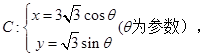 直线
直线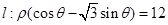
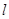 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程; 轴的正半轴重合.
轴的正半轴重合.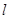 的参数方程为:
的参数方程为: (t为参数),曲线
(t为参数),曲线 的极坐标方程为:
的极坐标方程为: .
. 、
、 两点,求
两点,求 值.
值. (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r=
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r= cos(θ+
cos(θ+ ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长. 必过点( )
必过点( ) D.(3,7)
D.(3,7) 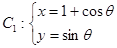
 为参数
为参数 ,在曲线
,在曲线 上求一点
上求一点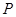 ,使它到直线
,使它到直线
 为参数
为参数