Question

已知曲线y=和这条曲线上的一点P(2,),判断曲线y=x在点P处是否有切线,如果有,求出切线方程.

Answer 1

分析一:本题考查导数的几何意义.函数y=f(x)在点P处的切线的斜率是否存在的问题,可转化为割线PQ的斜率的极限是否存在的问题.

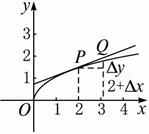
解法一:在曲线y=上点P附近取一点Q,设Q点的横坐标为2+Δx,则点Q的纵坐标为

.

∴函数的增量Δy=.

∴割线PQ的斜率k_PQ=.

∴Δx→0时,k_PQ有极限为,这表明曲线y=在点P处有切线,且切线的斜率是,由点斜式可得切线方程为y-=(x-2),即x-4y+2=0.

分析二: 函数y=是可导的.对y=求导,就得到曲线y=的切线的斜率.在x=2处切线的斜率就是导函数在该点处的函数值.

解法二:y′=()′=.

∴y′|_x=2==.

由点斜式可得在P点处切线的方程为y-=(x-2),

即x-4y+2=0.

点评 本题主要考查导数的几何意义.过曲线上一点P,若存在切线,则切线是过该点的割线PQ的极限位置,它反映了事物之间量变到质变的辩证关系.