题目内容
曲线y=x2+1上点P处的切线与曲线y=-2x2-1也相切,求点P的坐标.
分析：利用导数的几何意义.
解：设P点坐标为(a,a2+1),由y=x2+1,得y′=2x.过P点的切线方程为y-(a2+1)=2a(x-a),
即y=2ax-a2+1,由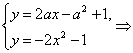
2x2+2ax-a2+2=0.
由相切知Δ=0,即a=±
,
∴P点为(
,
),( 
,
).
练习册系列答案
相关题目
题目内容
曲线y=x2+1上点P处的切线与曲线y=-2x2-1也相切,求点P的坐标.
分析：利用导数的几何意义.
解：设P点坐标为(a,a2+1),由y=x2+1,得y′=2x.过P点的切线方程为y-(a2+1)=2a(x-a),
即y=2ax-a2+1,由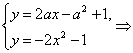2x2+2ax-a2+2=0.
由相切知Δ=0,即a=±,
∴P点为(,),( ,).
x2-1|上点的最短距离为( )
B