题目内容
(本小题满分12分)已知公差不为0的等差数列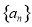 的前
的前 项和为
项和为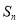 ,
, 且
且 成等比数列.
成等比数列.
(1)求数列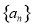 的通项公式;
的通项公式;
(2)设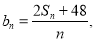 数列
数列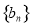 的最小项是第几项,并求出该项的值.
的最小项是第几项,并求出该项的值.
(1) ;(2)最小项第4项,最小值23.
;(2)最小项第4项,最小值23.
【解析】
试题分析:(1)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解,基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.(3)解题时要善于类比要能正确区分等差、等比的性质,不要把两者的性质搞混了.
试题解析:【解析】
(1)设公差为 ,则有
,则有 ,
,
即 或
或 (舍),
(舍),
(2) ,
,
 ,
,
当且仅当 时取
时取 号,即
号,即 时取
时取 号.
号.
考点:1、等差数列的通项公式;2、等差数列的前 项和公式;3、基本不等式的应用.
项和公式;3、基本不等式的应用.
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 万元用于修复和加强民俗文化基础设施.据测算,修复好部落民俗文化基础设施后,任何一个月(每月均按
万元用于修复和加强民俗文化基础设施.据测算,修复好部落民俗文化基础设施后,任何一个月(每月均按 天计算)中第
天计算)中第 天的游客人数
天的游客人数 近似满足
近似满足 (单位:千人),第
(单位:千人),第 天游客人均消费金额
天游客人均消费金额 近似满足
近似满足 (单位:元).
(单位:元). 天的日旅游收入
天的日旅游收入 (单位:千元,
(单位:千元, ,
, )的表达式;
)的表达式; %作为每一天应回收的投资成本,试问该部落至少经过几年就可以收回全部投资成本.
%作为每一天应回收的投资成本,试问该部落至少经过几年就可以收回全部投资成本.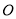 的两弦
的两弦 和
和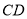 交于点
交于点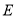 ,
,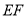 ∥
∥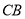 ,
,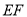 交
交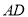 的延长线于点
的延长线于点 ,
,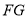 切圆
切圆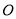 于点
于点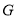 .
. 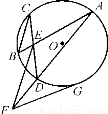
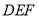 ∽△
∽△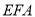 ;
;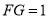 ,求
,求 ,则输出
,则输出 的值为( )
的值为( )
 的两弦
的两弦 和
和 交于点
交于点 ,
, ∥
∥ ,
, 交
交 的延长线于点
的延长线于点 ,
, 切圆
切圆 于点
于点 .
. 
 ∽△
∽△ ;
; ,求
,求 的外接圆半径为1,圆心为
的外接圆半径为1,圆心为 ,且
,且 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,则输出
,则输出 的值为( )
的值为( )
 上的两点
上的两点 、
、 到焦点的距离之和为6,则线段
到焦点的距离之和为6,则线段 的中点到
的中点到 轴的距离为 .
轴的距离为 . ,集合
,集合 ,则
,则 .
.