题目内容
(本小题满分10分)选修4—1,几何证明选讲
如图所示,圆 的两弦
的两弦 和
和 交于点
交于点 ,
, ∥
∥ ,
, 交
交 的延长线于点
的延长线于点 ,
, 切圆
切圆 于点
于点 .
.

(1)求证:△ ∽△
∽△ ;
;
(2)如果 ,求
,求 的长.
的长.
(1)证明见解析;(2)
【解析】
试题分析:(1)判断三角形相似:一是平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似;二是如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似;三是如果两个三角形的两组对应边的比相等,并且相应的夹角相等, 那么这两个三角形相似;四是如果两个三角形的三组对应边的比相等,那么这两个三角形相似;五是对应角相等,对应边成比例的两个三角形叫做相似三角;(2)切割线定理:切割线定理,是圆幂定理的一种,从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
试题解析:证明:
(1)  ∽
∽
(2) ∽
∽
又因为 为切线,则
为切线,则
所以, .
.
考点:1、三角形相似的判断;2、求线段的弦长.
考点分析: 考点1:圆的切线的性质及判定定理 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (
( ,
, ,
, ).
). 的最小值;
的最小值; 对满足条件的一切实数
对满足条件的一切实数 ,
, ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是( )
所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是( )
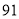 ,
, 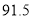 B.
B.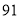 ,
, 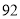 C.
C.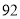
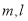 ,平面
,平面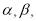 且
且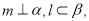 给出下列命题:
给出下列命题: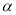 ∥
∥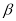 ,则
,则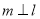 ;
; 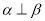 ,则
,则 ∥
∥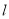 ;
; 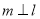 ,则
,则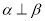 ;
;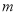 ∥
∥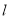 ,则
,则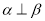 . 其中正确的命题的个数是( )
. 其中正确的命题的个数是( ) 则“
则“ ”是“方程
”是“方程 表示开口向右的抛物线”的( )
表示开口向右的抛物线”的( )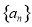 的前
的前 项和为
项和为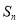 ,
, 且
且 成等比数列.
成等比数列.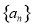 的通项公式;
的通项公式;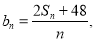 数列
数列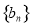 的最小项是第几项,并求出该项的值.
的最小项是第几项,并求出该项的值. ,平面
,平面 且
且 给出下列命题:
给出下列命题: ∥
∥ ,则
,则 ; ②若
; ②若 ,则
,则 ∥
∥ ; ③若
; ③若 ,则
,则 ;
; ∥
∥ ,则
,则 . 其中正确的命题的个数是( )
. 其中正确的命题的个数是( ) 均为非零向量,下列四个条件中,使
均为非零向量,下列四个条件中,使 成立的必要条件是( ).
成立的必要条件是( ). B.
B. C.
C. D.
D. 且
且
 是实系数一元二次方程
是实系数一元二次方程 的一个根,则
的一个根,则 .
.