题目内容
4．
已知不等式组$\left\{{\begin{array}{l}{3x-y-3≥0}\\{x-2y-1≤0}\\{2x+y-7≤0}\end{array}}\right.$表示的区域为D，（1）在坐标系中作出区域D（用阴影部分表示）；
（2）若在可行域D内，使目标函数z=kx-y的取得最小值的最优解有无数个，求实数k的取值范围．
分析 （1）根据二元一次不等式组表示平面区域，即可作出对应的图象．
（2）根据目标函数的几何意义，利用数形结合进行求解即可．
解答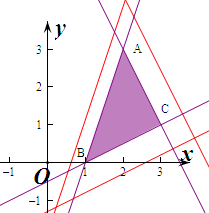 
解：（1）作出不等式组对应的平面区域如图：
（2）由z=kx-y得y=kx-z，
若k=0，则y=-z，此时目标函数取得最小值的解只有一个，不满足条件．
若k＞0，若目标函数z=kx-y的取得最小值的最优解有无数个，
则目标函数对应的直线与AB：3x-y-3=0平行，
此时k=3，
若k＜0，若目标函数z=kx-y的取得最小值的最优解有无数个，
则目标函数对应的直线与AC：2x+y-7=0平行，
此时k=-2，
综上k=3或-2．
点评 本题主要考查线性规划的应用，利用数形结合以及目标函数的几何意义是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．考察下列每组对象：
①非常大的正整数全体；
②小于100的所有整数；
③某校2014年秋季入学的所有长头发同学；
④平面直角坐标系第一象限内的所有点；
⑤大于0且小于1的所有无理数．
其中能构成集合的个数为（ ）
①非常大的正整数全体；
②小于100的所有整数；
③某校2014年秋季入学的所有长头发同学；
④平面直角坐标系第一象限内的所有点；
⑤大于0且小于1的所有无理数．
其中能构成集合的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
如图在平行四边形ABCD中，M，N分别为DC，BC的中点，已知$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow b$，试用$\overrightarrow a$，$\overrightarrow{b}$表示$\overrightarrow{AC}，\overrightarrow{BD}，\overrightarrow{AM，}\overrightarrow{AN}$，$\overrightarrow{NM}，\overrightarrow{MB}$．