题目内容
16.在△ABC中,角A,B,C所对的边分别为a,b,c,其中C角为钝角.cos(A+B-C)=$\frac{1}{4}$,a=2,$\frac{{sin({B+A})}}{sinA}$=2.(1)求cosC的值;
(2)求b的长.
分析 (1)利用三角形内角和定理及诱导公式可得-cos2C=$\frac{1}{4}$,由倍角公式化简即可求得cosC的值.
(2)由已知及由正弦定理可得c,由余弦定理c2=a2+b2-2abcosC,即可解得b的值.
解答 解:(1)∵cos(A+B-C)=cos[(π-C)-C]=cos(π-2C)=-cos2C=$\frac{1}{4}$,
∴解得:cos2C=2cos2C-1=-$\frac{1}{4}$,解得:cos2C=$\frac{3}{8}$,由C角为钝角,解得:cosC=-$\frac{\sqrt{6}}{4}$.
(2)∵$\frac{{sin({B+A})}}{sinA}$=2,a=2,
∴可得sinC=2sinA,由正弦定理可得:c=2a=4,
∴由余弦定理c2=a2+b2-2abcosC,可得:16=4+b2-2×$2×b×(-\frac{\sqrt{6}}{4})$,解得:b=$\sqrt{6}$.
点评 本题主要考查了三角形内角和定理,诱导公式,倍角公式,正弦定理,余弦定理的应用,熟练掌握公式是解题的关键,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
7.设f(x)、g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)-f(x)g′(x)>0且g(-3)=0.则不等式f(x)g(x)<0的解集是( )
| A. | (-∞,-3)∪(0,3) | B. | (-3,0)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(3,+∞) |
11.已知等差数列{an}的公差为d,前n项和为Sn,若S6>S7>S5,则下列命题错误的是( )
| A. | d<0 | B. | S11>0 | ||
| C. | {Sn}中的最大项为S11 | D. | |a6|>|a7| |
8.已知向量$\overrightarrow{a}$=(0,2$\sqrt{3}$),b=(1,$\sqrt{3}$),则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -3 |
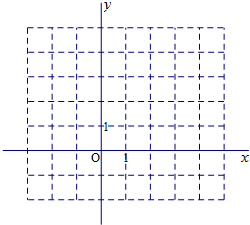 已知不等式组$\left\{{\begin{array}{l}{3x-y-3≥0}\\{x-2y-1≤0}\\{2x+y-7≤0}\end{array}}\right.$表示的区域为D,
已知不等式组$\left\{{\begin{array}{l}{3x-y-3≥0}\\{x-2y-1≤0}\\{2x+y-7≤0}\end{array}}\right.$表示的区域为D,