Question

已知可行域

y≥0 x-y+2≥0 x+y-2≤0

的外接圆C与x轴交于点A₁、A₂，双曲线E以线段A₁A₂为实轴，离心率e=

6

2

．则圆C的方程是

 

；双曲线E的方程是

 

．

Answer 1

分析：根据题意，作出可行域

y≥0 x-y+2≥0 x+y-2≤0

，求出三个交点的坐标，分析可得这是一个等腰直角三角形的区域，由等腰直角三角形的性质，可得其外接圆的圆心与半径，进而可得其方程，又有圆C与x轴交于点A₁、A₂，可得A₁、A₂的坐标，可得a的值；且已知双曲线的离心率，可得c的值，进而有双曲线的性质，可得b的值，即可得双曲线的标准方程．

解答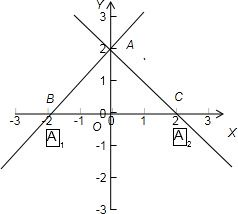：解：根据题意，作出可行域

y≥0 x-y+2≥0 x+y-2≤0

，
设其交点分别为A（0，2），B（-2，0），C（2，0）；
分析可得，△ABC是等腰直角三角形，且BC是斜边；
其外接圆的圆心在斜边的中点，即原点，半径为斜边的一半，即2；
故这个圆的方程为x²+y²=4；
其与x轴交于点A₁、A₂，就是B、C两点，
则双曲线E的实轴端点为（-2，0），（2，0）；
则a=2，
其离心率e=

6

2

，故c=

6

；
则b=

2

；
其焦点在x轴上，
故其方程为

x2

4

-

y2

2

=1；
故答案为：x²+y²=4；

x2

4

-

y2

2

=1．

点评：本题考查圆的方程、双曲线的标准方程的求法，要求学生掌握常见的求法，如定义法、待定系数法．