题目内容
设f(n)=cos(
+
),则f(1)+f(2)+…+f(2006)=______.
| nπ |
| 2 |
| π |
| 4 |
分别令x=1,2,3,4,5,…,n.得到一个规律:从第一项开始,连续每四项之和为0,而2006÷4=501余数为2,所以
f(1)+f(2)+…+f(2006)=-
-
=-
.
故答案为:-
f(1)+f(2)+…+f(2006)=-
| ||
| 2 |
| ||
| 2 |
| 2 |
故答案为:-
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
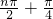 ),则f(1)+f(2)+…+f(2006)=________.
),则f(1)+f(2)+…+f(2006)=________. ),则f(1)+f(2)+…+f(2006)= .
),则f(1)+f(2)+…+f(2006)= .