题目内容
设f(n)=cos(| nπ |
| 2 |
| π |
| 4 |
分析:令n=1,得到f(1)=cos(
+
)=-sin
=-
;令x=2,得到f(2)=cos(π+
)=-cos
=-
;令x=3,得到f(3)=cos(
+
)=sin
=
;x=4,得到f(4)=cos(2π+
)=cos
=
;x=5,得到f(5)=cos(
+
)=-
,…,得到一个规律,利用2006除以4,看余数为几即可得到之和.
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 5π |
| 2 |
| π |
| 4 |
| ||
| 2 |
解答:解:分别令x=1,2,3,4,5,…,n.得到一个规律:从第一项开始,连续每四项之和为0,而2006÷4=501余数为2,所以
f(1)+f(2)+…+f(2006)=-
-
=-
.
故答案为:-
f(1)+f(2)+…+f(2006)=-
| ||
| 2 |
| ||
| 2 |
| 2 |
故答案为:-
| 2 |
点评:考查学生灵活运用诱导公式化简求值,会从特殊的值得到一般性的规律并应用规律求和.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
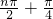 ),则f(1)+f(2)+…+f(2006)=________.
),则f(1)+f(2)+…+f(2006)=________. ),则f(1)+f(2)+…+f(2006)= .
),则f(1)+f(2)+…+f(2006)= .