题目内容
10、已知在正三棱锥P-ABC中,M,N分别为PA,BC中点,G为MN中点,求证:PG⊥BC.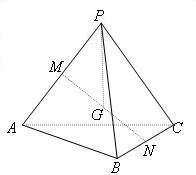

分析:要证明PG⊥BC,可以先证明BC⊥平面PMN,而要证明BC⊥平面PMN,我们可以证明BC与平面PMN中的两条相交直线PN,MN都垂直,由于三棱锥P-ABC为正三棱锥我们不难根据等腰三角形的性质,得到结论.
解答:证明:∵三棱锥P-ABC为正三棱锥
∴PB=PC
又∵N为BC中点,则PN⊥BC
又∵侧面PAB≌侧面PAC
∴MB=MC
∴MN⊥BC
又∵MN∩PN=N
∴BC⊥平面PMN
又∵PG?平面PMN
∴PG⊥BC
∴PB=PC
又∵N为BC中点,则PN⊥BC
又∵侧面PAB≌侧面PAC
∴MB=MC
∴MN⊥BC
又∵MN∩PN=N
∴BC⊥平面PMN
又∵PG?平面PMN
∴PG⊥BC
点评:线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
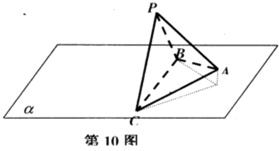 我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥、现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高h,边BC在平面上转动,若某个时刻它在平面α上的射影是等腰直角三角形,则h的取值范围是( )
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥、现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高h,边BC在平面上转动,若某个时刻它在平面α上的射影是等腰直角三角形,则h的取值范围是( )A、(0,
| ||||||||
B、(0,
| ||||||||
C、(0,
| ||||||||
D、(0,
|