题目内容
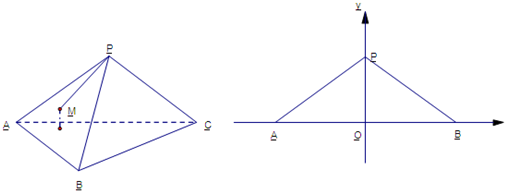
已知正三棱锥P-ABC,点P,A,B,C都在半径为
的球面上,若PA,PB,PC两两互相垂直,则正三棱锥P-ABC的高为 .
| 3 |
分析:由正三棱锥P-ABC的四个顶点均在半径为
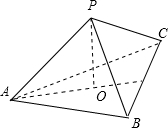
的球面上,且PA,PB,PC两两垂直,球直径等于以PA,PB,PC为棱的正方体的对角线,由此可求得棱锥的侧棱长与底面三角形的边长,过P作PO⊥平面ABC,则O为△ABC的中心,求出OA,利用勾股定理求出三棱锥P-ABC的高H.
| 3 |
解答:解:∵PA,PB,PC两两垂直,
又∵三棱锥P-ABC的四个顶点均在半径为
的球面上,
∴以PA,PB,PC为棱的正方体的对角线即为球的一条直径.
∴(2
)2=PA2+PB2+PC2=3PA2⇒PA=PB=PC=2,
底面正△ABC的边长为
=2
,
过P作PO⊥平面ABC,则O为△ABC的中心,OA=
×
×2
=
,
三棱锥P-ABC的高H=
=
.
故答案是
.
又∵三棱锥P-ABC的四个顶点均在半径为
| 3 |
∴以PA,PB,PC为棱的正方体的对角线即为球的一条直径.
∴(2
| 3 |
底面正△ABC的边长为
| 22+22 |
| 2 |
过P作PO⊥平面ABC,则O为△ABC的中心,OA=
| 2 |
| 3 |
| ||
| 2 |
| 2 |
2
| ||
| 3 |
三棱锥P-ABC的高H=
22-(
|
2
| ||
| 3 |
故答案是
2
| ||
| 3 |

点评:题考查的知识点是棱锥的外接球及棱锥的结构特征,其中根据已知条件,得到棱锥的外接球直径等于以PA,PB,PC为棱的正方体的对角线,是解答本题的关键.

练习册系列答案
相关题目
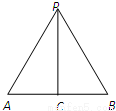
 已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为
已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为