题目内容
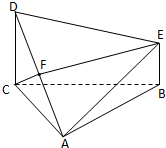 已知D、E分别在平面ABC的同侧,且DC⊥平面ABC,EB⊥平面ABC,DC=2,△ABC是边长为2的正三角形,F是AD中点.
已知D、E分别在平面ABC的同侧,且DC⊥平面ABC,EB⊥平面ABC,DC=2,△ABC是边长为2的正三角形,F是AD中点.(1)当BE等于多少时,EF∥平面ABC;
(2)当EF∥平面ABC时,求平面DAE和平面ABC所成的角.
分析:(1)取AC中点G,连接FG、BG,则FG∥DC∥BE,易知当BE=1时,BEFG为平行四边形,由线面平行的判定定理可得结论;
(2)由(1)知,当EF∥平面ABC时,BE=1,取BC中点O,过O作OZ⊥平面ABC,建立恰当的空间直角坐标系,转化为两平面的法向量的夹角可求得结果;
(2)由(1)知,当EF∥平面ABC时,BE=1,取BC中点O,过O作OZ⊥平面ABC,建立恰当的空间直角坐标系,转化为两平面的法向量的夹角可求得结果;
解答: 解:(1)取AC中点G,连接FG、BG,则FG∥DC∥BE,
解:(1)取AC中点G,连接FG、BG,则FG∥DC∥BE,
当BE=1时,有FG=BE,即BEFG为平行四边形,
故当BE=1时,EF∥BG,且BG?平面ABC,EF?平面ABC,
∴EF∥平面ABC;
(2)由(1)知,当EF∥平面ABC时,BE=1,取BC中点O,过O作OZ⊥平面ABC,
如图,建立空间直角坐标系,则A(
,0,0),B(0,1,0),E(0,1,1),D(0,-1,2),
平面ABC的法向量为
=(0,0,1),
设平面ADE法向量为
=(x,y,z),
=(-
,-1,2),
=(0,2,-1),
由
,得
,取z=2,则y=1,x=
,
∴
=(
,1,2),
∴cos<
,
>=
=
=
,则<
,
>=45°,
∴平面DAE和平面ABC所成角为45°或135°.
 解:(1)取AC中点G,连接FG、BG,则FG∥DC∥BE,
解:(1)取AC中点G,连接FG、BG,则FG∥DC∥BE,当BE=1时,有FG=BE,即BEFG为平行四边形,
故当BE=1时,EF∥BG,且BG?平面ABC,EF?平面ABC,
∴EF∥平面ABC;
(2)由(1)知,当EF∥平面ABC时,BE=1,取BC中点O,过O作OZ⊥平面ABC,
如图,建立空间直角坐标系,则A(
| 3 |
平面ABC的法向量为
| BE |
设平面ADE法向量为
| n |
| AD |
| 3 |
| DE |
由
|
|
| 3 |
∴
| n |
| 3 |
∴cos<
| BE |
| n |
| ||||
|
|
| 2 | ||
2
|
| ||
| 2 |
| BE |
| n |
∴平面DAE和平面ABC所成角为45°或135°.
点评:本题考查线面平行的判定、二面角的求解,考查空间向量在立体几何中的应用,考查学生的推理论证能力、空间想象能力.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
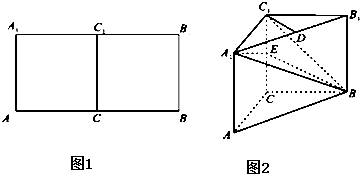

 的正△ABC,点D,E分别在边AB,AC上,且DE∥BC,以DE为折痕,把△ADE折起至△A'DE,使点A'在平面BCED上的射影H始终落在BC边上,记
的正△ABC,点D,E分别在边AB,AC上,且DE∥BC,以DE为折痕,把△ADE折起至△A'DE,使点A'在平面BCED上的射影H始终落在BC边上,记 ,则S的取值范围为 .
,则S的取值范围为 .