题目内容
已知α∈(| π |
| 2 |
| 3π |
| 2 |
| 3 |
| 4 |
分析:首先利用诱导公式得出tanα的值,然后根据同角三角函数的关系以及角的范围求出cosα和sina,再由二倍角的正弦公式求出结果.
解答:解:∵tan(7π-α)=-tanα=
∴tanα=-
,则
=-
,
∵sin2α+cos2α=1,α∈(
,
)
∴cosα=-
,sina=
∴sin2a=2sinαcosα=-
故答案为-
| 3 |
| 4 |
∴tanα=-
| 3 |
| 4 |
| sinα |
| cosα |
| 3 |
| 4 |
∵sin2α+cos2α=1,α∈(
| π |
| 2 |
| 3π |
| 2 |
∴cosα=-
| 4 |
| 5 |
| 3 |
| 5 |
∴sin2a=2sinαcosα=-
| 24 |
| 25 |
故答案为-
| 24 |
| 25 |
点评:本题考查了三角函数的诱导公式以及二倍角的正弦,解题过程中要注意角的范围,属于基础题.

练习册系列答案
相关题目
已知2≤x≤3,2x-1≤y≤2x,则
的最小值为( )
| y |
| x |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
 |=2,|
|=2,| |=3,
|=3, 与4
与4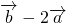 平行,求实数x的值.
平行,求实数x的值. |=2,|
|=2,| |+3,若(
|+3,若( )•(
)•( )=-53,则向量
)=-53,则向量 ,
, 的夹角是 .
的夹角是 . =2•
=2• ,
, =3•
=3• ,
, =4•
=4• ,….若
,….若 =8•
=8• (a,t均为正实数),类比以上等式,可推测a,t的值,则a+t= .
(a,t均为正实数),类比以上等式,可推测a,t的值,则a+t= .