题目内容
(2x-1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,则a2=( )
| A、60 | B、-60 |
| C、160 | D、15 |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于2,求出r的值,即可求得a2的值.
解答:
解:由题意可得,a2表示(2x-1)6 的展开式中x2的系数,
而(2x-1)6的展开式的通项公式为Tr+1=
•(-1)r•(2x)6-r,令6-r=2,求得 r=4,
可得a2=15×4=60,
故选:A.
而(2x-1)6的展开式的通项公式为Tr+1=
| C | r 6 |
可得a2=15×4=60,
故选:A.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
在△ABC中,
•
=7,|
-
|=6,则△ABC面积的最大值为( )
| AB |
| AC |
| AB |
| AC |
| A、24 | B、16 | C、12 | D、8 |
已知角α的终边过点P(x,-3)且cosα=-
,则x的值为( )
| ||
| 2 |
A、±3
| ||||
B、3
| ||||
C、-3
| ||||
D、-
|
已知△ABC中,tanA=-
,那么cosA等于( )
| 5 |
| 12 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知集合A={x|x2-2x-8<0},B={y|y=log2(x2+2)},则A∩B=( )
| A、(-2,-1] |
| B、[-1,4) |
| C、(-∞,4) |
| D、[1,4) |
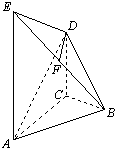 在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.