Question

【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量，对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分，每项评分最低分0分，最高分100分，每个景点总分为这五项得分之和，根据考核评分结果，绘制交通得分与安全得分散点图、交通得分与景点总分散点图如下：

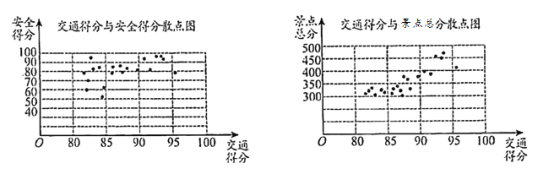
请根据图中所提供的信息，完成下列问题：

（I）若从交通得分前6名的景点中任取2个，求其安全得分都大于90分的概率；

（II）若从景点总分排名前6名的景点中任取3个，记安全得分不大于90分的景点个数为，求随机变量的分布列和数学期望；

（III）记该市26个景点的交通平均得分为安全平均得分为，写出和的大小关系？（只写出结果）

Answer 1

【答案】（I）；（II）分布列见解析，期望为；（III）

【解析】

（I）根据古典概型概率计算公式，计算出所求概率.

（II）利用超几何分布的知识求出分布列和数学期望.

（III）根据两种得分的数据离散程度进行判断.

（I）由图可知，交通得分前名的景点中，安全得分大于分的景点有个，所以从交通得分前名的景点中任取个，求其安全得分都大于分的概率为.

（II）结合两个图可知，景点总分排名前的的景点中，安全得分不大于分的景点有个，所以的可能取值为.

.

所以的分布列为:

所以.

（III）由图可知，个景点中，交通得分全部在分以上，主要集中在分附近，安全得分主要集中在分附近，且分一下的景点接近一半，故 .