题目内容
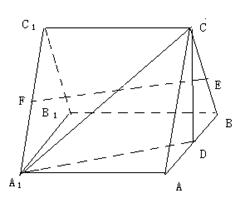
如图,在直三棱柱(即侧棱与底面垂直的三棱柱)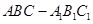 中,
中,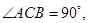
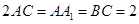 ,
,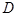 为
为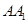 的中点
的中点
(I)求证:平面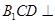 平面
平面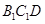 ;
;
(II)求 到平面
到平面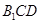 的距离.
的距离.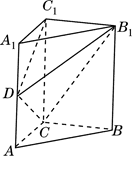
(I)略;(II)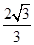 .
.
解析试题分析:(I)可以转化为证线面垂直(如转化为证明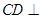 平面
平面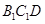 );(II)可利用等积法求点面距.设
);(II)可利用等积法求点面距.设 到平面
到平面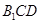 的距离为
的距离为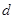 ,利用
,利用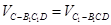 ,列出关于
,列出关于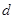 的方程
的方程 ,得
,得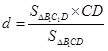 ,进而可求得
,进而可求得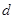 .
.
试题解析:(I)证明:∵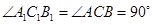 ,∴
,∴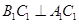 .
. 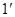
又由直三棱柱的性质知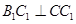 ,
, 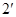
∴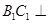 平面
平面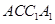 .
.
∴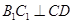 , ①
, ①
由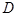 为
为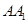 的中点,可知
的中点,可知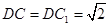 ,
,
∴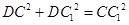 ,即
,即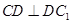 , ②
, ②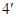
又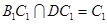 ③
③
由①②③可知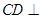 平面
平面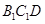 ,
, 
又 平面
平面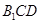 ,故平面
,故平面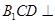 平面
平面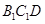 .
. 
(II)设 到平面
到平面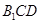 的距离为
的距离为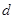 ,由(I)知CD⊥平面B1C1D,
,由(I)知CD⊥平面B1C1D,
所以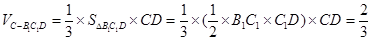

而由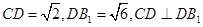 可得
可得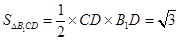
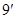
又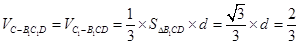
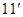
所以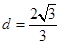
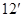
考点:1、空间面面垂直关系的证明;2、空间点面距.

练习册系列答案
相关题目
 中,点
中,点 是
是 的中点.
的中点.
 平面
平面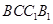 ;
; 平面
平面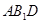 .
.
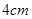 的正方形
的正方形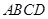 中,
中,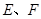 分别为
分别为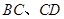 的中点,
的中点,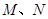 分别为
分别为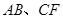 的中点,现沿
的中点,现沿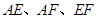 折叠,使
折叠,使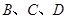 三点重合,重合后的点记为
三点重合,重合后的点记为 ,构成一个三棱锥.
,构成一个三棱锥.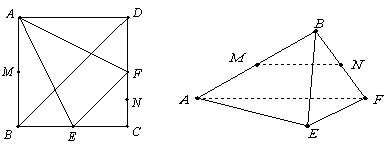
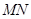 与平面
与平面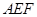 的位置关系,并给出证明;
的位置关系,并给出证明;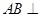 平面
平面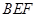 ;
;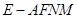 的体积.
的体积.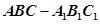 中,
中,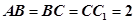 ,
,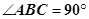 ,D是AC的中点.
,D是AC的中点.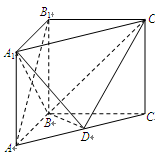
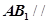 平面
平面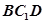 ;
;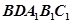 的体积.
的体积. 中,
中, ⊥底面
⊥底面 ,四边形
,四边形 ⊥
⊥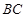 ,
, ,
,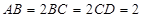 .
.
 ⊥平面
⊥平面 ;
;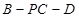 的余弦值为
的余弦值为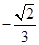 ,求
,求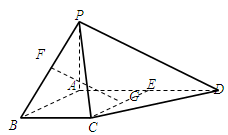
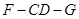 的正切值.
的正切值.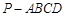 中,底面
中,底面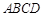 是矩形,四条侧棱长均相等.
是矩形,四条侧棱长均相等.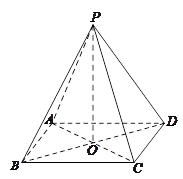
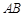
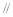 平面
平面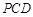 ;
;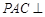 平面
平面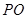 中,已知
中,已知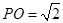 ,⊙O的直径
,⊙O的直径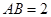 ,
,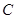 是
是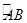 的中点,
的中点,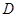 为
为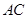 的中点.
的中点.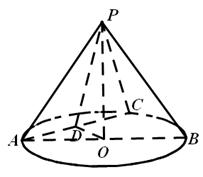
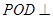 平面
平面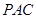 ;
;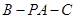 的余弦值.
的余弦值.