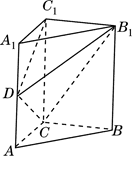
题目内容
如图,正三棱柱 中,点
中,点 是
是 的中点.
的中点.
(Ⅰ)求证:  平面
平面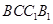 ;
;
(Ⅱ)求证: 平面
平面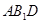 .
.
(Ⅰ)详见解析;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)欲证线面垂直,先考察线线垂直,易知 和
和 ,所以
,所以 平面
平面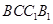 ;(Ⅱ)线面平行,先构造线线平行,根据中点,易想到构造三角形中位线,连接
;(Ⅱ)线面平行,先构造线线平行,根据中点,易想到构造三角形中位线,连接 ,设
,设 ,则可达到目的
,则可达到目的 .
.
试题解析:(Ⅰ)因为 是正三角形,而点
是正三角形,而点 是
是 的中点,所以
的中点,所以 ……………3分
……………3分
又三棱柱 是正三棱柱,所以
是正三棱柱,所以 面
面 ,
, 面
面 ,所以
,所以 ,
, ,所以
,所以 平面
平面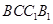 ;……………………………… 7分
;……………………………… 7分
(Ⅱ)连接 ,设
,设 ,则
,则 为
为 的中点,连接
的中点,连接 ,由
,由 是
是 的中点,
的中点,
得 ………11分
………11分
又 面
面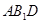 ,且
,且 面
面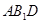 ,所以
,所以 平面
平面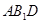 .………14分
.………14分
考点:直线与平面平行的判定、直线与平面垂直的判定.

练习册系列答案
相关题目
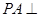 平面
平面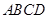 ,四边形
,四边形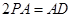 ,
,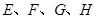 分别是线段
分别是线段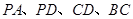 的中点.
的中点.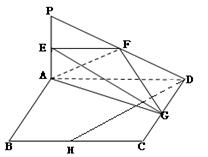
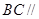 平面
平面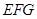 ;
;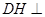 平面
平面 ;
;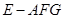 与四棱锥
与四棱锥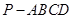 的体积比.
的体积比.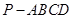 中,平面
中,平面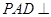 平面
平面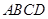 ,
,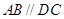 ,
,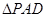 是等边三角形,已知
是等边三角形,已知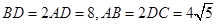 .
.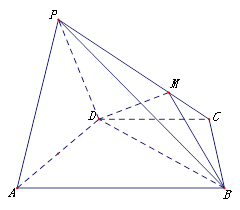
 是
是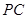 上的一点,证明:平面
上的一点,证明:平面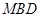 ;
;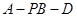 的余弦值.
的余弦值.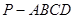 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱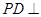 底面ABCD,
底面ABCD,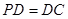 ,E是PC的中点.
,E是PC的中点.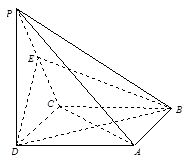
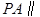 平面EDB;
平面EDB;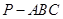 中,
中,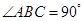 ,
,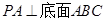
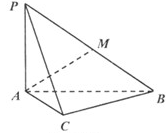
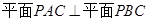 ;
;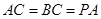 ,
,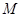 是
是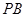 的中点,求
的中点,求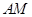 与平面
与平面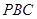 所成角的正切值
所成角的正切值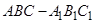 中,
中,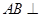 侧面
侧面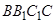 ,已知
,已知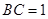 ,
,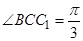 ,
,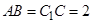 .
.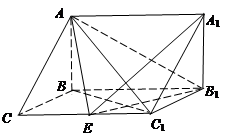
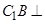 平面
平面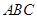 ;
;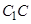 (不包含端点
(不包含端点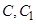 )上确定一点
)上确定一点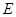 的位置,使得
的位置,使得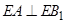 ;
;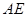 和平面
和平面
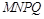 为平行四边形;
为平行四边形;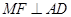 .
. AB.
AB.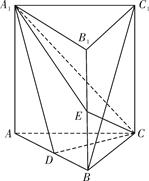
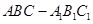 中,
中,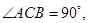
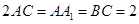 ,
,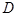 为
为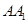 的中点
的中点
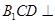 平面
平面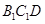 ;
; 到平面
到平面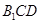 的距离.
的距离.