题目内容
如图,四棱锥 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形, 平面
平面 ,
,
 ,
, ,
, 为
为 的中点,
的中点, 在棱
在棱 上.
上.

(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
【答案】
(1)证明过程详见解析;(2) .
.
【解析】
试题分析:本题主要以四棱锥为几何背景考查线线平行、线线垂直、线面垂直、线面平行、面面垂直以及三棱锥的体积等基础知识,考查学生的空间想象能力和逻辑推理能力.第一问,在 中,
中, 和
和 都是中点,所以
都是中点,所以 ,利用面面垂直的判定可以判断平面
,利用面面垂直的判定可以判断平面 平面
平面 ,因为
,因为 垂直2个面的交线,所以
垂直2个面的交线,所以 垂直平面
垂直平面 ,即
,即 平面
平面 ,因为
,因为 垂直
垂直 和
和 ,所以利用线面垂直的判定得
,所以利用线面垂直的判定得 平面
平面 ,所以
,所以 面内的线
面内的线 ;第二问,将所求三棱锥进行等体积转换,法一是利用
;第二问,将所求三棱锥进行等体积转换,法一是利用 ,法二是利用
,法二是利用 ,进行求解.
,进行求解.
试题解析:(Ⅰ)连接 ,
,
 为
为 的中点,
的中点, ,
,
因为 平面
平面 ,
, 平面
平面 ,
,
所以平面 平面
平面 ,
,
且平面 平面
平面 ,
, ,
, 平面
平面
所以 平面
平面 , 4分
, 4分

 ,又
,又
 ,
, 平面
平面 ,
, 平面
平面 ,
,
所以 . 6分
. 6分

(Ⅱ)由(Ⅰ)知 ,
,
 平面
平面 ,所以
,所以 平面
平面 ,
,
又 平面
平面 ,所以
,所以 即为点
即为点 与平面
与平面 的距离,
的距离, ,而
,而 , 10分
, 10分
 12分
12分
解法二
(Ⅱ)由(Ⅰ)知 ,
,
 平面
平面 ,所以
,所以 平面
平面 ,
,
所以 即为点
即为点 与平面
与平面 的距离
的距离
 .
.
考点:1.线面垂直的判定;2.线面平行的判定;3.面面垂直的判定;4.等体积法.

练习册系列答案
相关题目
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD= 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 平面
平面 ;
②若二面角
;
②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.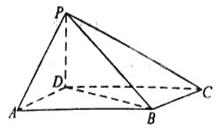
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,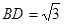 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 底面
底面 ;
; 求二面角
求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,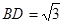 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。