题目内容
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,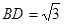 ,
, ⊥底面
⊥底面 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。

【答案】
(1)∵ ∴
∴
又∵ ⊥底面
⊥底面 ∴
∴
又∵ ∴
∴ 平面
平面
而 平面
平面
∴平面 平面
平面 ………………………………………5分
………………………………………5分
(2)由(1)所证, 平面
平面
所以∠ 即为二面角P-BC-D的平面角,即∠
即为二面角P-BC-D的平面角,即∠

而 ,所以
,所以 …………………………………………7分
…………………………………………7分
分别以 、
、 、
、 为
为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系。
轴建立空间直角坐标系。
则 ,
, ,
, ,
,

所以, ,
, ,
,
设平面 的法向量为
的法向量为 ,则
,则

即 可解得
可解得
∴ 与平面
与平面 所成角的正弦值为
所成角的正弦值为
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD= 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 平面
平面 ;
②若二面角
;
②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.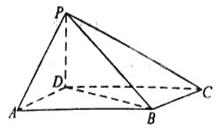
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 底面
底面 ;
; 求二面角
求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,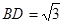 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。