题目内容
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD=| 39 |
| 3 |
(1)求异面直线SA与BD所成角的正切值;
(2)求证:二面角A-SD-C的大小.
分析:(1)过A作AO∥BD交CD的延长线于点O,连接BO交AD于点E,再连接OS,可得∠SAO是异面直线SA与所成的角.再利用解三角形的有关知识得到SE=6,OE=BE=3,在△SEO中由余弦定理可得:SO=3
,然后在△SOA中由长度关系得到SO⊥OA,进而求出线面角的正切值.
(2)在△SOE中由长度关系得到SO⊥OE,又SO⊥OA,可得SO⊥平面ABCD,所以平面SOC⊥平面ABCD,过A作AF⊥OD,得到AF⊥平面SOD,作AN⊥SD,并且交SD与点N,连FN,由三垂线定理可得:FN⊥SD,根据二面角的平面角的定义可得:∠FNA为二面角A-SD-O的平面角,进而利用解三角形的有关知识求出二面角的平面角.
| 3 |
(2)在△SOE中由长度关系得到SO⊥OE,又SO⊥OA,可得SO⊥平面ABCD,所以平面SOC⊥平面ABCD,过A作AF⊥OD,得到AF⊥平面SOD,作AN⊥SD,并且交SD与点N,连FN,由三垂线定理可得:FN⊥SD,根据二面角的平面角的定义可得:∠FNA为二面角A-SD-O的平面角,进而利用解三角形的有关知识求出二面角的平面角.
解答:解:(1)过A作AO∥BD交CD的延长线于点O,连接BO交AD于点E,再连接OS,
∴∠SAO是异面直线SA与所成的角.…(2分)
∵OABD是平行四边形,∴E是AD的中点.
∵SA=SD=
,∴SE⊥AD,
又∵底面ABCD是菱形,并且∠DAB=60°,
∴BE⊥AD,
∴∠SEB是二面角S-AD-B的平面角,即∠SEB=120°,
∴∠SEO=60°.…(4分)
∵SA=SD=
,AD=2
,
∴SE=6,OE=BE=3,
∴在△SEO中由余弦定理可得:SO2=SE2+OE2-2SE•OE•cos60°⇒SO=3
.
在△SOA中,SO=3
,SA=
,OA=2
,SO2+OA2=SA2⇒SO⊥OA,
∴tan∠SAO=
=
=
;…(6分)
所以异面直线SA与BD所成角的正切值为
.
(2)在△SOE中,SO=3
,SE=6,OE=3,SO2+OE2=SE2⇒SO⊥OE
由(1)可得:在△SOA中,SO⊥OA,
∴SO⊥平面ABCD,SO?平面SOC
故平面SOC⊥平面ABCD,…(8分)
过A作AF⊥OD,
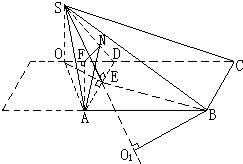
∴AF⊥平面SOD,
作AN⊥SD,并且交SD与点N,连FN,
∴由三垂线定理可得:FN⊥SD,
∴根据二面角的平面角的定义可得:∠FNA为二面角A-SD-O的平面角…(10分)
由题意可得:AF=ADsin60°=3,
在△SAD中根据等面积可得:
×AD×SE=
×SD×AN,即
× 2
×6=
×
×AN,
所以AN=
=
,
所以sin∠FNA=
=
=
.
故二面角A-SD-C的大小为π-arcsin
.…(12分)
∴∠SAO是异面直线SA与所成的角.…(2分)
∵OABD是平行四边形,∴E是AD的中点.
∵SA=SD=
| 39 |
又∵底面ABCD是菱形,并且∠DAB=60°,
∴BE⊥AD,
∴∠SEB是二面角S-AD-B的平面角,即∠SEB=120°,
∴∠SEO=60°.…(4分)
∵SA=SD=
| 39 |
| 3 |
∴SE=6,OE=BE=3,
∴在△SEO中由余弦定理可得:SO2=SE2+OE2-2SE•OE•cos60°⇒SO=3
| 3 |
在△SOA中,SO=3
| 3 |
| 39 |
| 3 |
∴tan∠SAO=
| OS |
| OA |
3
| ||
2
|
| 3 |
| 2 |
所以异面直线SA与BD所成角的正切值为
| 3 |
| 2 |
(2)在△SOE中,SO=3
| 3 |
由(1)可得:在△SOA中,SO⊥OA,
∴SO⊥平面ABCD,SO?平面SOC
故平面SOC⊥平面ABCD,…(8分)
过A作AF⊥OD,

∴AF⊥平面SOD,
作AN⊥SD,并且交SD与点N,连FN,
∴由三垂线定理可得:FN⊥SD,
∴根据二面角的平面角的定义可得:∠FNA为二面角A-SD-O的平面角…(10分)
由题意可得:AF=ADsin60°=3,
在△SAD中根据等面积可得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 39 |
所以AN=
12
| ||
|
12
| ||
| 13 |
所以sin∠FNA=
| AF |
| AN |
| 3 | ||||
|
| ||
| 4 |
故二面角A-SD-C的大小为π-arcsin
| ||
| 4 |
点评:本题主要考查空间中的二面角的平面角与线面角,而空间角解决的关键是做角,其步骤是:首先是结合图形的结构及题设条件正确的作出空间角,再证明此角是所求角,然后利用解三角形的有关知识求出空间角,也可以根据几何体的结构特征建立空间直角坐标系利用向量的有关知识解决空间角等问题.

练习册系列答案
相关题目
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 平面
平面 ;
②若二面角
;
②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.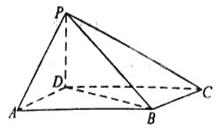
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,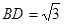 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 底面
底面 ;
; 求二面角
求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,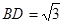 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。