题目内容

已知函数 $数学公式$ ．求使f（x）+g（x） $数学公式$ 成立的所有x的集合．

解：因为 $\text{[math]}$ ，所以f（x）+g（x）=2sinx，
又f（x）•g（x）=sin²x-3cos²x，
所以 $\text{[math]}$ ? $\text{[math]}$
即4sinx≥sin²x-3（1-sin²x）?4sin²x-4sinx-3≤0，
解得 $\text{[math]}$ ．
解得： $\text{[math]}$ ．
分析：求出f（x）的表达式，推出f（x）+g（x） $\text{[math]}$ 的表达式，然后纠错sinx的不等式，求出x的集合即可．
点评：本题考查两角和的正弦函数平方差公式的应用，考查三角函数的值域的应用，考查计算能力．

练习册系列答案

高效练习系列答案

训练与检测完全试卷系列答案

每课一练（福建）系列答案

智能达标AB卷系列答案

智慧金卷26套系列答案

单元加期末冲刺100分系列答案

高效智能课时作业系列答案

高效课堂互动英语系列答案

初中全程导学导练系列答案

期末总复习系列答案

相关题目

已知f（x）=loga

，（a＞0，且a≠1）．
（1）求f（x）的定义域．
（2）证明f（x）为奇函数．
（3）求使f（x）＞0成立的x的取值范围．

已知函数f（x）=sin(x-

)，g(x)=2sin2x
（Ⅰ）若α是第一象限角，且f（α）=

，求g（α）的值；
（Ⅱ）求使f（x）≥g（x）成立的x的取值集合．

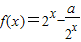，将y=f（x）的图象向右平移两个单位，得到y=g（x）的图象．
（1）求函数y=g（x）的解析式；
（2）若函数y=h（x）与函数y=g（x）的图象关于直线y=1对称，求函数y=h（x）的解析式；
（3）设

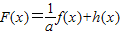，设F（x）的最小值为m．是否存在实数a，使

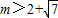，若存在，求出a的取值范围，若不存在，说明理由．

．
求使f（x）+g（x）

成立的所有x的集合．