题目内容
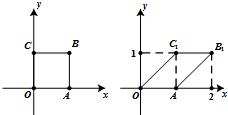（2013•泉州模拟）如图，单位正方形区域OABC在二阶矩阵M的作用下变成平行四边形OAB1C1区域．（Ⅰ）求矩阵M；
（Ⅱ）求M2，并判断M2是否存在逆矩阵？若存在，求出它的逆矩阵．
分析：（I）利用待定系数法，先假设所求的变换矩阵M=
，再利用点C（0，1）、A（1，0）分别变换成点C1（1，1）、A（1，0），可构建方程组，从而得解．
（II）先利用矩阵的乘方求出M2，再直接利用求逆矩阵的公式可求即得．
|
（II）先利用矩阵的乘方求出M2，再直接利用求逆矩阵的公式可求即得．
解答：解：（Ⅰ）设M=
，由
=
，得a=1，c=0，
由
=
，得b=1，d=1，
∴M=
．
（Ⅱ）M2=
=
，
∵|M2|=1≠0，∴M2存在逆矩阵，
M2的逆矩阵为
．
|
|
|
|
由
|
|
|
∴M=
|
（Ⅱ）M2=
|
|
|
∵|M2|=1≠0，∴M2存在逆矩阵，
M2的逆矩阵为
|
点评：本题以变换为依托，考查矩阵及其逆矩阵，关键是利用待定系数法，利用矩阵的乘法公式．
练习册系列答案
相关题目
（2013•泉州模拟）如图，等腰梯形ABCD中，AB∥CD且AB=2，AD=1，DC=2x（x∈（0，1））．以A，B为焦点，且过点D的双曲线的离心率为e1；以C，D为焦点，且过点A的椭圆的离心率为e2，则e1+e2的取值范围为 （ ）
（2013•泉州模拟）设全集U=R，A={x|x（x+3）＜0}，B={x|x＜-1}，则图中阴影部分表示的集合为（ ）