题目内容
（1）∵2
a2n+1+3
∴（a
n+1+2an）（2an+1-an）=0，∵{an}的各项均为正数，∴2an+1-an=0 即：an+1=
，∴{an}是以
为公比的等比数列，由a2+a4=2a3+
得。
a1=
∴an=（
又由Sn=n2得bn=2n-1
（2）Tn=
∴Tn<
(3)由cn=-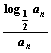
,得cn=-n•2n≥
得T/=(1-n)2n+1-2, 解答n≥6.
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
（1）∵2a2n+1+3∴（an+1+2an）（2an+1-an）=0，∵{an}的各项均为正数，∴2an+1-an=0 即：an+1=，∴{an}是以为公比的等比数列，由a2+a4=2a3+得。
a1=∴an=（又由Sn=n2得bn=2n-1
（2）Tn=∴Tn<
(3)由cn=-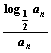,得cn=-n•2n≥
得T/=(1-n)2n+1-2, 解答n≥6.
名校课堂系列答案
如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f（f（0））=