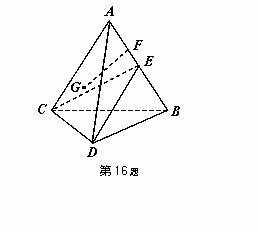
题目内容
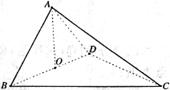
如图,四面体中,是的中点,和都是等边三角形,.
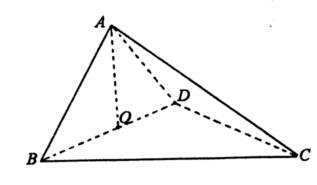 (1)求异面直线与直线所成的角
(1)求异面直线与直线所成的角
(2)求点到平面的距离.
解法一:(I)连结![]() ,
, ![]() 和
和![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,又
,又![]() ,
, ![]() ,
,
在![]() 中,
中, ![]()
![]() ,
,
![]() ,即
,即![]()
![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() BC,∴异面直线AO与直线BC所成的角为
BC,∴异面直线AO与直线BC所成的角为![]() . 6分
. 6分
(Ⅱ)显然B到到平面![]() 的距离是点
的距离是点![]() 到平面
到平面![]() 的距离的两倍,设点
的距离的两倍,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
, ![]() ,
, ![]() , 在
, 在![]() 中,
中,![]() ,
,
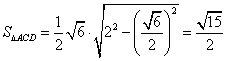 ,
, ![]()
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .∴点B到平面
.∴点B到平面![]() 的距离为
的距离为![]() . 12分
. 12分
法二:(I)同解法一…………………………………………………………6分
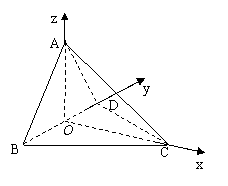 (Ⅱ)以
(Ⅱ)以![]() 为原点,如图建立空间直角坐标系,
为原点,如图建立空间直角坐标系,
则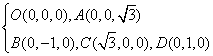
设平面![]() 的法向量为
的法向量为![]() 又
又![]()
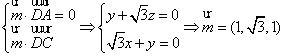 …………10分
…………10分
设![]() 与
与![]() 夹角为
夹角为![]() ,则
,则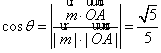 ,设
,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,![]() 到平面
到平面![]() 的距离为
的距离为![]() ,显然B到到平面
,显然B到到平面![]() 的距离是点
的距离是点![]() 到平面
到平面![]() 的距离的两倍,∴点B到平面
的距离的两倍,∴点B到平面![]() 的距离为
的距离为![]() .…12分
.…12分

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 中,
中, ,
, 是
是 的中点.
的中点.
 平面
平面 ;
; 为
为 的重心,
的重心, 是线段
是线段 上一点,且
上一点,且 .求证:
.求证: 平面
平面 中,
中, ,点
,点 分别是
分别是 的中点.
求证:
的中点.
求证: 平面
平面 ;
; 平面
平面 .
.