题目内容
若p：x2-1＞0，q：（x+1）（x-2）＞0，则﹁p是﹁q的 条件（填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”其中一个）．
分析：先化简p，q，然后求出﹁p，﹁q，利用充分条件和必要条件的定义进行判断．
解答：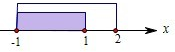
解：由x2-1＞0，解得x＞1或x＜-1，∴p：x＞1或x＜-1，﹁p：-1≤x≤1．
由（x+1）（x-2）＞0，解得x＞2或x＜-1，∴q：x＞2或x＜-1，﹁q：-1≤x≤2．
∴﹁p是﹁q的充分不必要条件．
故答案为：充分不必要条件．
解：由x2-1＞0，解得x＞1或x＜-1，∴p：x＞1或x＜-1，﹁p：-1≤x≤1．由（x+1）（x-2）＞0，解得x＞2或x＜-1，∴q：x＞2或x＜-1，﹁q：-1≤x≤2．
∴﹁p是﹁q的充分不必要条件．
故答案为：充分不必要条件．
点评：本题主要考查充分条件和必要条件的判断，以及非p之间的关系，利用数形结合是解决此类问题的基本方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列命题正确的有
①用相关指数R2来刻画回归效果越小，说明模型的拟合效果越好；
②命题p：“?x0∈R，x02-x0-1＞0”的否定?p：“?x∈R，x2-x-1≤0”；
③设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=p，则P(-1＜ξ＜0)=
-p；
④回归直线一定过样本中心（
，
）．（ ）
①用相关指数R2来刻画回归效果越小，说明模型的拟合效果越好；
②命题p：“?x0∈R，x02-x0-1＞0”的否定?p：“?x∈R，x2-x-1≤0”；
③设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=p，则P(-1＜ξ＜0)=
| 1 |
| 2 |
④回归直线一定过样本中心（
. |
| x |
. |
| y |
| A、1个 | B、2个 | C、3个 | D、4个 |
设随机变量η服从正态分布N（1，σ2），若P（η＜-1）=0.2，则函数f(x)=
x3+x2+η2x没有极值点的概率是（ ）
| 1 |
| 3 |
| A、0.2 | B、0.3 |
| C、0.7 | D、0.8 |