题目内容
若函数
，（a＞0且a≠1）的值域为R，则实数a的取值范围是 ．
【答案】分析：函数
，（a＞0且a≠1）的值域为R，则其真数在实数集上不恒为正，将这一关系转化为不等式求解参数的范围即可．
解答：解：函数
，（a＞0且a≠1）的值域为R，其真数在实数集上不恒为正，
即
不恒成立，即存在x∈R使得
≤4，又a＞0且a≠1
故可求
的最小值，令其小于等于4
∵
∴
4，解得a≤4，
故实数a的取值范围是（0，1）∪（1，4]
故应填（0，1）∪（1，4]
点评：考查存在性问题的转化，请读者与恒成立问题作比较，找出二者逻辑关系上的不同．
，（a＞0且a≠1）的值域为R，则其真数在实数集上不恒为正，将这一关系转化为不等式求解参数的范围即可．解答：解：函数
，（a＞0且a≠1）的值域为R，其真数在实数集上不恒为正，即
不恒成立，即存在x∈R使得≤4，又a＞0且a≠1故可求
的最小值，令其小于等于4∵
∴
4，解得a≤4，故实数a的取值范围是（0，1）∪（1，4]
故应填（0，1）∪（1，4]
点评：考查存在性问题的转化，请读者与恒成立问题作比较，找出二者逻辑关系上的不同．
练习册系列答案
相关题目
（其中a＞0且a≠1，a为实数常数）．
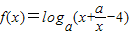，（a＞0且a≠1）的值域为R，则实数a的取值范围是 ．
，（a＞0且a≠1）的值域为R，则实数a的取值范围是 ．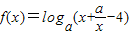
，（a＞0且a≠1）的值域为R，则实数a的取值范围是 ．