题目内容
已知函数 (其中a>0且a≠1,a为实数常数).
(其中a>0且a≠1,a为实数常数).(1)若f(x)=2,求x的值(用a表示);
(2)若a>1,且atf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围(用a表示).
【答案】分析:(1)首先对自变量x分x<0和x≥0两种情况去掉函数内的绝对值符号,然后分别令f(x)=2,就可求出x的值.
(2)根据a>1和t∈[1,2]的条件,对不等式进行等价转化,将参数m分离,从而转化成函数求最值问题,最终确定m的取值范围.
解答:解:(1)当x<0时f(x)=0,当x≥0时, .….(2分)
.….(2分)
由条件可知, ,即a2x-2•ax-1=0解得
,即a2x-2•ax-1=0解得 …(6分)
…(6分)
∵ax>0,∴ …..(8分)
…..(8分)
(2)当t∈[1,2]时, …(10分)
…(10分)
即 m(a2t-1)≥-(a4t-1)∵a>1,t∈[1,2]∴a2t-1>0,∴m≥-(a2t+1)…(13分)
∵t∈[1,2],∴a2t+1∈[a2+1,a4+1]∴-(a2t+1)∈[-1-a4,-1-a2]
故m的取值范围是[-1-a2,+∞)….(16分)
点评:本题主要考查了指数的运算性质和函数恒成立问题,函数恒成立问题一般的方法是直接构造函数求最值或分离常数之后在构造函数求最值两种策略,因为函数表达式中含有绝对值所以,先考虑取绝对值.
(2)根据a>1和t∈[1,2]的条件,对不等式进行等价转化,将参数m分离,从而转化成函数求最值问题,最终确定m的取值范围.
解答:解:(1)当x<0时f(x)=0,当x≥0时,
 .….(2分)
.….(2分)由条件可知,
 ,即a2x-2•ax-1=0解得
,即a2x-2•ax-1=0解得 …(6分)
…(6分)∵ax>0,∴
 …..(8分)
…..(8分)(2)当t∈[1,2]时,
 …(10分)
…(10分)即 m(a2t-1)≥-(a4t-1)∵a>1,t∈[1,2]∴a2t-1>0,∴m≥-(a2t+1)…(13分)
∵t∈[1,2],∴a2t+1∈[a2+1,a4+1]∴-(a2t+1)∈[-1-a4,-1-a2]
故m的取值范围是[-1-a2,+∞)….(16分)
点评:本题主要考查了指数的运算性质和函数恒成立问题,函数恒成立问题一般的方法是直接构造函数求最值或分离常数之后在构造函数求最值两种策略,因为函数表达式中含有绝对值所以,先考虑取绝对值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.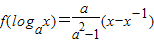 ,其中a>0且a≠1.
,其中a>0且a≠1.