题目内容
已知椭圆 和圆
和圆 :
: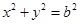 ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B.

(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;
(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时, 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
 和圆
和圆 :
: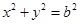 ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 
(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得
 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时,
 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.(1) ,
,
(2) 为定值,定值是
为定值,定值是 .
.
 ,
,
(2)
 为定值,定值是
为定值,定值是 .
. 试题分析:解:(1)(ⅰ)∵ 圆
 过椭圆的焦点,圆
过椭圆的焦点,圆 :
: 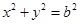 ,∴
,∴  ,
,∴
 ,
,  ,
,∴
 . 4分
. 4分(ⅱ)由
 及圆的性质,可得
及圆的性质,可得 ,∴
,∴
∴

∴
 ,
,  . 8分
. 8分 (2)

设
 ,则
,则 , 整理得
, 整理得
 ∴
∴ 方程为:
方程为: , 10分
, 10分 方程为:
方程为: .
.从而直线AB的方程为:
 . 12分
. 12分令
 ,得
,得 ,令
,令 ,得
,得 ,
,∴
 ,
,∴
 为定值,定值是
为定值,定值是 . 16
. 16点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 离心率为
离心率为 直线
直线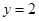 与C的两个交点间的距离为
与C的两个交点间的距离为
 ;
;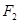 的直线l与C的左、右两支分别相交有A、B两点,且
的直线l与C的左、右两支分别相交有A、B两点,且 证明:
证明:
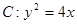 上的不同两点,F为抛物线C的焦点,若
上的不同两点,F为抛物线C的焦点,若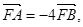 则直线AB的斜率为
则直线AB的斜率为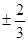 B.
B.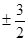 C.
C.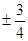 D.
D.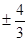
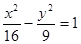 的右顶点为焦点的抛物线的标准方程为 ( )
的右顶点为焦点的抛物线的标准方程为 ( )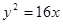
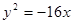

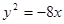
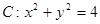 上一点P,动点Q满足
上一点P,动点Q满足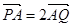 ,则点Q的轨迹方程为( )
,则点Q的轨迹方程为( )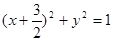
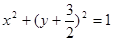

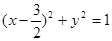
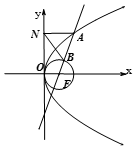
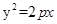 (p>0)的焦点为F,A为C上的点,以F为圆心,
(p>0)的焦点为F,A为C上的点,以F为圆心,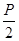 为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠
为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠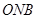 = .
= .
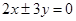 为渐近线,且经过点
为渐近线,且经过点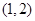 的双曲线标准方程是
的双曲线标准方程是  和圆
和圆 的极坐标方程分别为
的极坐标方程分别为 ,则经过两圆圆心的直线的直角坐标方程为_________.
,则经过两圆圆心的直线的直角坐标方程为_________. (
( >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。