题目内容
15.一种放射性物质1000克,每经过一年,剩余的质量约为原来的95%,设计一个算法计算10年后剩余的质量.并画出程序框图.分析 本题选择指数函数型的函数模型解决.经过一年,剩留物质约是原来的1000×95%,经过二年,剩留物质约是原来的1000×(95%)2,…十年后,剩留物质的量为1000×(95%)10,由已知中程序的功能为用循环结构计算1000×(95%)10的值,为累乘运算,且要反复累加10次,可令循环变量的初值为1,终值为10,步长为1,由此确定程序框图.
解答 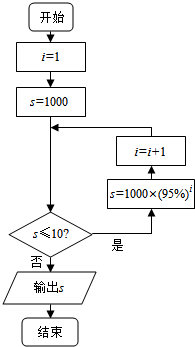 解:算法如下:
解:算法如下:
第一步:设i的值为1;
第二步:设s的值为1000;
第三步:如果i≤10执行第四步,
否则转去执行第七步;
第四步:计算s*(95%)i并将结果代替s;
第五步:计算i+1并将结果代替i;
第六步:转去执行第三步;
第七步:输出s的值并结束算法.
程序框图如图:
点评 本小题主要考查函数模型的选择与应用、指数函数等基础知识,考查设计程序框图解决实际问题,考查数学建模能力,属于基础题.

练习册系列答案
相关题目