题目内容
(本小题满分14分)
已知函数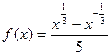 ,
,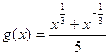 ;
;
(Ⅰ)证明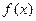 是奇函数;
是奇函数;
(Ⅱ)证明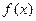 在(-∞,-1)上单调递增;
在(-∞,-1)上单调递增;
(Ⅲ)分别计算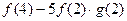 和
和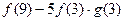 的值,由此概括出涉及函数
的值,由此概括出涉及函数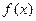 和
和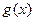 的对所有不等于零的实数
的对所有不等于零的实数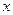 都成立的一个等式,并加以证明
都成立的一个等式,并加以证明
已知函数
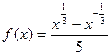 ,
,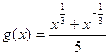 ;
;(Ⅰ)证明
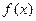 是奇函数;
是奇函数;(Ⅱ)证明
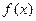 在(-∞,-1)上单调递增;
在(-∞,-1)上单调递增;(Ⅲ)分别计算
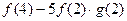 和
和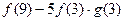 的值,由此概括出涉及函数
的值,由此概括出涉及函数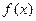 和
和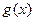 的对所有不等于零的实数
的对所有不等于零的实数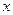 都成立的一个等式,并加以证明
都成立的一个等式,并加以证明略
解:(Ⅰ)∵函数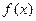 的定义域为(-∞,0)∪(0,+∞),是关于原点对称的;
的定义域为(-∞,0)∪(0,+∞),是关于原点对称的;
又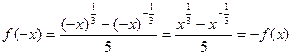
∴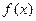 是奇函数. ……………………………………………………………(4分)
是奇函数. ……………………………………………………………(4分)
(Ⅱ)设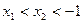 , 则:
, 则: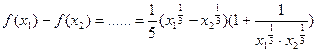 ,
,
∵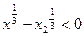 ,
,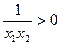 ,
,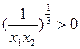 ,
,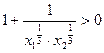 ,
,
∴ .即
.即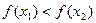 且
且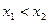
∴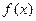 在
在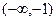 上单调递增. …(8分)
上单调递增. …(8分)
(Ⅲ)算得: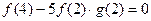 ;
; 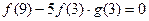 ;
;
由此概括出对所有不等于零的实数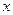 都成立的等式是:
都成立的等式是: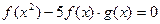 …(12分)
…(12分)
下面给予证明:∵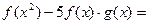
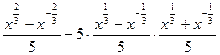
=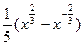 -
-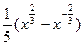 =0
=0
∴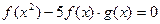 对所有不等于零的实数
对所有不等于零的实数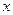 都成立. ………………(14分)
都成立. ………………(14分)
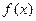 的定义域为(-∞,0)∪(0,+∞),是关于原点对称的;
的定义域为(-∞,0)∪(0,+∞),是关于原点对称的;又
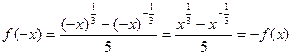
∴
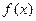 是奇函数. ……………………………………………………………(4分)
是奇函数. ……………………………………………………………(4分)(Ⅱ)设
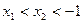 , 则:
, 则: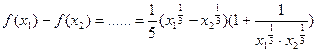 ,
,∵
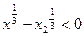 ,
,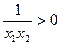 ,
,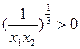 ,
,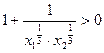 ,
, ∴
 .即
.即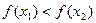 且
且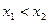
∴
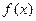 在
在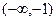 上单调递增. …(8分)
上单调递增. …(8分)(Ⅲ)算得:
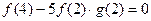 ;
; 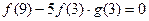 ;
; 由此概括出对所有不等于零的实数
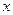 都成立的等式是:
都成立的等式是: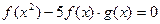 …(12分)
…(12分)下面给予证明:∵
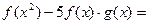
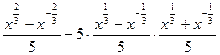
=
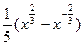 -
-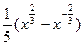 =0
=0∴
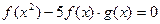 对所有不等于零的实数
对所有不等于零的实数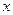 都成立. ………………(14分)
都成立. ………………(14分)
练习册系列答案
相关题目
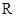 上的函数
上的函数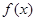 满足
满足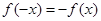 ,当
,当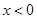 时,
时,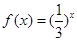 ,则
,则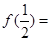
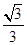
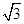
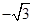
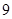
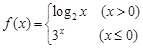 ,则
,则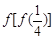 的值是( ).
的值是( ).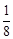 C. 9 D.
C. 9 D. 
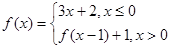 ,则
,则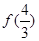 的值为( )
的值为( )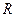 的函数
的函数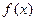 是偶函数,当
是偶函数,当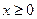 时,
时,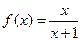 .
.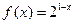 在区间
在区间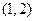 上有解
上有解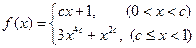 ,若
,若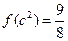 ,则不等式
,则不等式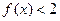 的解集为
的解集为 ,则
,则 = .
= .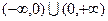 上的奇函数
上的奇函数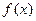 ,在
,在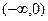 单调递增,且
单调递增,且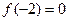 ,则不等式
,则不等式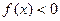 的解集是_________________
的解集是_________________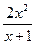 ,函数g(x)=asin(
,函数g(x)=asin(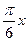 )-2a+2(a>0),若存在x1,x2∈[0,1]使得f(x1)=g(x2)成立,则实数a的取值范围是( )
)-2a+2(a>0),若存在x1,x2∈[0,1]使得f(x1)=g(x2)成立,则实数a的取值范围是( )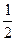 ,
, ]
]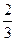 ,1]
,1]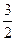 ]
]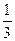 ,2]
,2]