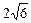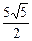题目内容
(本小题满分12分)
已知椭圆C: 的长轴长为4.
的长轴长为4.
(1)若以原点为圆心,椭圆短半轴长为半径的圆与直线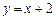 相切,求椭圆焦点坐标;
相切,求椭圆焦点坐标;
(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆交于M,N两点,直线PM,PN的斜率乘积为 ,求椭圆的方程.
,求椭圆的方程.
已知椭圆C:
 的长轴长为4.
的长轴长为4.(1)若以原点为圆心,椭圆短半轴长为半径的圆与直线
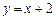 相切,求椭圆焦点坐标;
相切,求椭圆焦点坐标;(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆交于M,N两点,直线PM,PN的斜率乘积为
 ,求椭圆的方程.
,求椭圆的方程.(1)两个焦点坐标为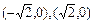
(2)椭圆方程为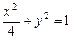
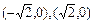
(2)椭圆方程为
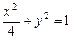
解:(1)由直线与圆相切知: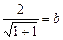 ,得
,得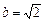 …………………………………(2分)
…………………………………(2分)
由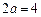 ,得
,得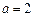 ,则
,则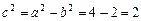
∴两个焦点坐标为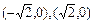 ……………………………………………(4分)
……………………………………………(4分)
(2)由于过原点的直线L与椭圆的两个交点关于原点对称
不妨设: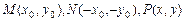
∵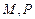 在椭圆上,∴满足
在椭圆上,∴满足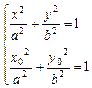 ,相减得:
,相减得: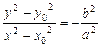 ……………(8分)
……………(8分)
由题意知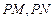 斜率存在,则
斜率存在,则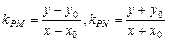 ………………………(10分)
………………………(10分)
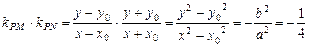
由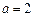 ,得
,得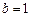 ,∴所求的椭圆方程为
,∴所求的椭圆方程为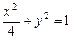 ……………………………(12分)
……………………………(12分)
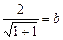 ,得
,得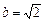 …………………………………(2分)
…………………………………(2分)由
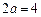 ,得
,得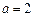 ,则
,则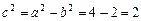
∴两个焦点坐标为
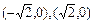 ……………………………………………(4分)
……………………………………………(4分)(2)由于过原点的直线L与椭圆的两个交点关于原点对称
不妨设:
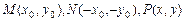
∵
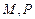 在椭圆上,∴满足
在椭圆上,∴满足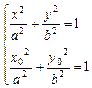 ,相减得:
,相减得: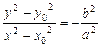 ……………(8分)
……………(8分)由题意知
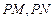 斜率存在,则
斜率存在,则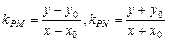 ………………………(10分)
………………………(10分)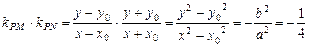
由
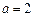 ,得
,得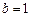 ,∴所求的椭圆方程为
,∴所求的椭圆方程为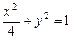 ……………………………(12分)
……………………………(12分)
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
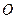 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为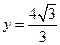 ,离心率
,离心率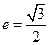 ,
,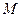 是椭圆上的动点.
是椭圆上的动点.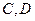 的坐标分别是
的坐标分别是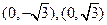 ,求
,求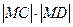 的最大值;
的最大值;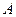 的坐标为
的坐标为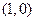 ,
,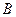 是圆
是圆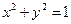 上的点,点
上的点,点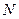 是点
是点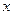 轴上的射影,点
轴上的射影,点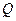 满足条件:
满足条件: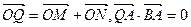 ,求线段
,求线段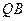 的中点
的中点 的轨迹方程.
的轨迹方程.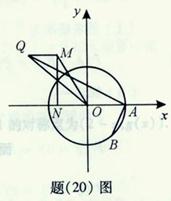
 ,短轴长为4,(1)求椭圆的方程;
,短轴长为4,(1)求椭圆的方程; 两点,求AB的中点坐标及其弦长|AB|。
两点,求AB的中点坐标及其弦长|AB|。  :
: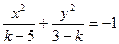 ,则“
,则“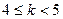 ”是“曲线C表示焦点在
”是“曲线C表示焦点在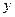 轴上的椭圆”的______________条件.
轴上的椭圆”的______________条件.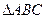 中顶点
中顶点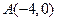 和顶点
和顶点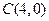 ,顶点
,顶点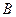 在椭圆
在椭圆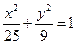 上,则
上,则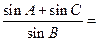
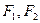 分别是椭圆
分别是椭圆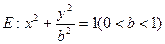 的左、右焦点,过
的左、右焦点,过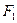 的直线
的直线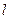 与
与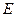 相交于
相交于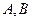 两点,且
两点,且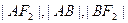 成等差数列,则
成等差数列,则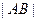 的长为 .
的长为 .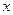 轴上的椭圆
轴上的椭圆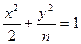 的离心率为
的离心率为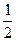 ,则
,则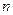 =( )
=( )
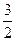
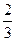
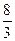
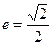 ,点
,点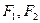 分别为椭圆的左、右焦点,过右焦点
分别为椭圆的左、右焦点,过右焦点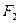 且垂直于长轴的弦长为
且垂直于长轴的弦长为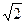
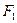 作直线
作直线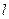 ,交椭圆于
,交椭圆于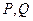 两点,若
两点,若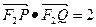 ,求直线
,求直线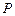 是椭圆
是椭圆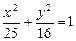 上一动点,
上一动点,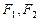 是椭圆的两个焦点,
是椭圆的两个焦点,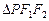 的内切圆半径为
的内切圆半径为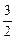 ,则当点点
,则当点点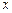 轴上方时,点
轴上方时,点