题目内容
已知 (x∈R),
(x∈R), ,且
,且 .
.
求:
(1) 的值;
的值;
(2)若A,B,C为△ABC的三个内角,A,B为锐角,且 ,
, ,求cosC的值.
,求cosC的值.
解: .
.
(1) .
.
(2)∵ ,
, ,
,
∴ ,
,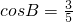 .
.
∵A,B为锐角,∴ ,
, .
.
∴cosC=cos(π-A-B)=-cos(A+B)=-coaAcosB+sinAsinB=- ×
× +
+ ×
× =-
=-
分析:先利用向量数量积运算的性质,求函数f(x)的解析式,再利用两角差的正弦公式,将函数化为y=Asin(ωx+φ)型函数,
(1)将x= 代入函数解析式,利用特殊角三角函数值即可得
代入函数解析式,利用特殊角三角函数值即可得 的值;
的值;
(2)先将已知函数值进行化简,得角A、B的三角函数值,再利用两角和的余弦公式代入求值即可
点评:本题主要考查了向量数量积的运算性质,两角和差的三角公式的运用,y=Asin(ωx+φ)型函数的性质,属基础题
 .
.(1)
 .
.(2)∵
 ,
, ,
,∴
 ,
,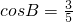 .
.∵A,B为锐角,∴
 ,
, .
.∴cosC=cos(π-A-B)=-cos(A+B)=-coaAcosB+sinAsinB=-
 ×
× +
+ ×
× =-
=-
分析:先利用向量数量积运算的性质,求函数f(x)的解析式,再利用两角差的正弦公式,将函数化为y=Asin(ωx+φ)型函数,
(1)将x=
 代入函数解析式,利用特殊角三角函数值即可得
代入函数解析式,利用特殊角三角函数值即可得 的值;
的值;(2)先将已知函数值进行化简,得角A、B的三角函数值,再利用两角和的余弦公式代入求值即可
点评:本题主要考查了向量数量积的运算性质,两角和差的三角公式的运用,y=Asin(ωx+φ)型函数的性质,属基础题

练习册系列答案
相关题目
 (x∈R),
(x∈R), ,且
,且 .
. 的值;
的值; ,
, ,求cosC的值.
,求cosC的值. (x∈R),
(x∈R), ,且
,且 .求:
.求: 的值;
的值; ,
, ,求cosC的值.
,求cosC的值.