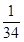题目内容
已知当x∈R时,函数y=f(x)满足f( 2.5+x )=f( 1.5+x )+
,且f(1)=
,则f(2010)的值为( )
| 1 |
| 3 |
| 4 |
| 3 |
分析:根据当x∈R时,函数y=f(x)满足f( 2.5+x )=f( 1.5+x )+
,令x=n,(n∈N*,n≥2),可以推出数列{f(n)}是等差数列,利用等差数列的通项公式即可求得结果.
| 1 |
| 3 |
解答:解:∵当x∈R时,函数y=f(x)满足f( 2.5+x )=f( 1.5+x )+
,
∴n∈N*,n≥2,有f( n )=f[ 2.5+(n-2.5 )]=f( 1.5+(n-2.5 ))+
=f( n-1 )+
,
∴数列{f(n)}是以f(1)为首项,
为公差的等差数列,
∴f(2010)=
+
(2010-1)=671
故选C.
| 1 |
| 3 |
∴n∈N*,n≥2,有f( n )=f[ 2.5+(n-2.5 )]=f( 1.5+(n-2.5 ))+
| 1 |
| 3 |
| 1 |
| 3 |
∴数列{f(n)}是以f(1)为首项,
| 1 |
| 3 |
∴f(2010)=
| 4 |
| 3 |
| 1 |
| 3 |
故选C.
点评:本题考查函数与数列的结合,由函数y=f(x)满足f( 2.5+x )=f( 1.5+x )+
,构造一个等差数列是解题的关键,属难题.
| 1 |
| 3 |

练习册系列答案
相关题目
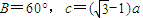 .
.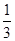 ,且f(1)=1,则f(100)
,且f(1)=1,则f(100)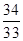 B.
B.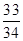 C.34 D.
C.34 D.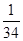
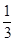 ,且f(1)=1,则f(100)的值为(
)
,且f(1)=1,则f(100)的值为(
)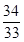 B.
B.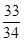 C.34 D.
C.34 D.