题目内容
定义在R上的偶函数 ,对任意x1,x2∈[0,+∞),(x1≠x2),有
,对任意x1,x2∈[0,+∞),(x1≠x2),有 ,
,
则 ( )
A. | B. |
C. | D. |
A
解析试题分析:∵任意x1,x2∈[0,+∞),(x1≠x2),有 ,∴函数f(x)在[0,+∞)单调递减,∵3>2>1,∴f(3)<f(2)<f(1),又函数
,∴函数f(x)在[0,+∞)单调递减,∵3>2>1,∴f(3)<f(2)<f(1),又函数 为偶函数,∴f(-2)="f(2)" ,∴
为偶函数,∴f(-2)="f(2)" ,∴ ,故选A
,故选A
考点:本题考查了函数的性质
点评:熟练掌握函数的单调性和奇偶性是解决此类问题的关键,属基础题

练习册系列答案
相关题目
已知函数f(x)=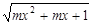 的定义域是一切实数,则m的取值范围是( )
的定义域是一切实数,则m的取值范围是( )
| A.0<m≤4 | B.0≤m≤1 | C.m≥4 | D.0≤m≤4 |
设函数 ,若
,若 则函数
则函数 的最小值是 ( )
的最小值是 ( )
A. | B. | C. | D. |
若 的解析式为 ( )
的解析式为 ( )
| A.3 | B. | C. | D. |
已知函数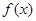 是定义在
是定义在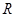 上的奇函数,且满足
上的奇函数,且满足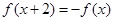 ,当
,当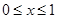 时,
时,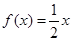 ,则满足
,则满足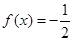 的
的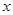 的值是( )
的值是( )
A.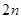 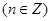 | B.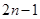 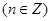 |
C.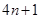 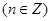 | D.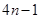 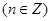 |
为了得到函数 的图像,可将函数
的图像,可将函数 的图像上所有的点的( )
的图像上所有的点的( )
A.纵坐标缩短为原来的 ,横坐标不变,再向右平移1个单位 ,横坐标不变,再向右平移1个单位 |
B.纵坐标缩短为原来的 ,横坐标不变,再向左平移1个单位 ,横坐标不变,再向左平移1个单位 |
| C.横坐标伸长为原来的2倍,纵坐标不变,再向左平移1个单位 |
| D.横坐标伸长为原来的2倍,纵坐标不变,再向右平移1个单位 |
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,且|x1|<|x2|,则有( )
| A.a>0,b>0,c<0,d>0 |
| B.a<0,b>0,c<0,d>0 |
| C.a<0,b<0,c>0,d>0 |
| D.a>0,b<0,c>0,d<0 |
 的图象如图所示,则导函数
的图象如图所示,则导函数 的图象可能是 ( )
的图象可能是 ( )
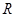 上的函数
上的函数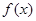 满足:
满足: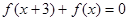 ,且函数
,且函数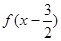 为奇函数。给出以下3个命题:
为奇函数。给出以下3个命题: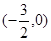 对称;
对称; 轴对称。
轴对称。