题目内容
已知点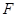 是椭圆
是椭圆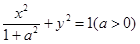 的右焦点,点
的右焦点,点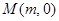 、
、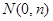 分别是
分别是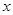 轴、
轴、
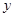 轴上的动点,且满足
轴上的动点,且满足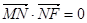 .若点
.若点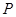 满足
满足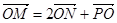 .
.
(Ⅰ)求点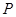 的轨迹
的轨迹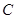 的方程;
的方程;
(Ⅱ)设过点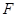 任作一直线与点
任作一直线与点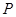 的轨迹交于
的轨迹交于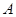 、
、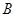 两点,直线
两点,直线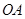 、
、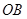 与直线
与直线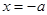 分别交
分别交
于点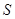 、
、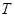 (
(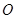 为坐标原点),试判断
为坐标原点),试判断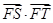 是否为定值?若是,求出这个定值;若不是,
是否为定值?若是,求出这个定值;若不是,
请说明理由.
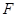 是椭圆
是椭圆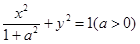 的右焦点,点
的右焦点,点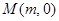 、
、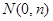 分别是
分别是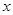 轴、
轴、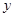 轴上的动点,且满足
轴上的动点,且满足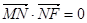 .若点
.若点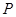 满足
满足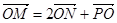 .
.(Ⅰ)求点
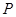 的轨迹
的轨迹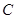 的方程;
的方程;(Ⅱ)设过点
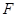 任作一直线与点
任作一直线与点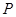 的轨迹交于
的轨迹交于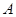 、
、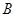 两点,直线
两点,直线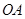 、
、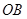 与直线
与直线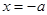 分别交
分别交于点
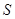 、
、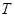 (
(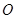 为坐标原点),试判断
为坐标原点),试判断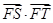 是否为定值?若是,求出这个定值;若不是,
是否为定值?若是,求出这个定值;若不是,请说明理由.
(Ⅰ) (Ⅱ)
(Ⅱ)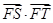 的值是定值,且定值为
的值是定值,且定值为
 (Ⅱ)
(Ⅱ)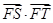 的值是定值,且定值为
的值是定值,且定值为试题分析:(Ⅰ)
 椭圆
椭圆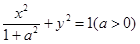 右焦点
右焦点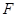 的坐标为
的坐标为 ,
,  .
. ,
, 由
由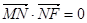 ,得
,得 .
. 设点
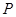 的坐标为
的坐标为 ,由
,由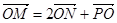 ,有
,有 ,
, 代入
代入 ,得
,得 .
. (Ⅱ)解法一:设直线
 的方程为
的方程为 ,
, 、
、 ,
,则
 ,
, .
. 由
 ,得
,得 , 同理得
, 同理得 .
.  ,
, ,则
,则 .
. 由
 ,得
,得 ,
, .
. 则
 .
. 因此,
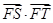 的值是定值,且定值为
的值是定值,且定值为 .
. 解法二:①当
 时,
时,  、
、 ,则
,则 ,
,  .
.由
 得点
得点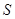 的坐标为
的坐标为 ,则
,则 .
.由
 得点
得点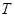 的坐标为
的坐标为 ,则
,则 .
. .
. ②当
 不垂直
不垂直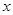 轴时,设直线
轴时,设直线 的方程为
的方程为 ,
, 、
、 ,同解
,同解法一,得
 .
. 由
 ,得
,得 ,
, .
. 则
 .
. 因此,
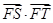 的值是定值,且定值为
的值是定值,且定值为 .
. 点评:解决此类题目的关键是熟练掌握求轨迹方程的方法(消参法),以及设点利用点表示
有关的向量的表达式即可,此题对计算能力要求较高.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
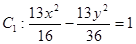 ,点
,点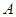 、
、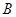 分别为双曲线
分别为双曲线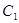 的左、右焦点,动点
的左、右焦点,动点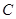 在
在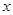 轴上方.
轴上方.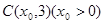 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以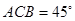 ,求△
,求△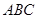 的外接圆的方程;
的外接圆的方程;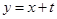 上任取一点
上任取一点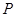 ,从点
,从点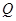 . 问是否存在一个定点
. 问是否存在一个定点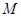 ,恒有
,恒有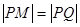 ?请说明理由.
?请说明理由.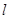 :
: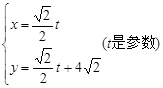 上的点向圆C:
上的点向圆C: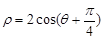 引切线,
引切线,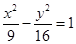 的一个焦点到一条渐近线的距离为______________
的一个焦点到一条渐近线的距离为______________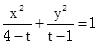 表示曲线
表示曲线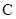 ,给出以下命题:
,给出以下命题: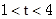 ,则曲线
,则曲线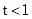 或
或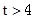 ;
;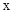 轴上的椭圆,则
轴上的椭圆,则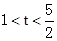 .
.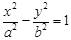 (a>0,b>0) 的左、右焦点,过F1的直线与
(a>0,b>0) 的左、右焦点,过F1的直线与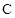 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
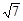 ,0),直线
,0),直线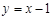 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为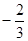 ,则此双曲线的方程是 .
,则此双曲线的方程是 . 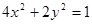 的一个焦点
的一个焦点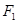 的直线与椭圆交于
的直线与椭圆交于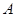 、
、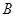 两点,则
两点,则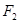 构成
构成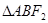 ,那么
,那么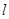 经过抛物线
经过抛物线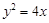 的焦点F,且与抛物线相交于A、B两点.
的焦点F,且与抛物线相交于A、B两点.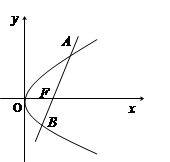
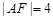 ,求点A的坐标;
,求点A的坐标; ,求线段AB的长.
,求线段AB的长.