题目内容
6.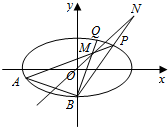 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.(1)求直线AB的方程;
(2)若点P为椭圆C上异于A,B的任意一点,直线AP,BP分别交直线y=x于点M,N,直线BM交椭圆于另外一点Q.
①证明:|OM||ON|为定值;
②证明:A、Q、N三点共线.
分析 (1)设出E(t,t),得到A(2t,2t+1),把A的坐标代入椭圆方程求得t,则直线AB的方程可求;
(2)①设P(x0,y0),则$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}=1$,然后分别求出直线AP、BP的方程,与直线y=x联立求得M,N的横坐标,由|OM||ON|=$\sqrt{2}|{x}_{M}|•\sqrt{2}|{x}_{N}|$化简得答案;
②设出直线BM:y=kx-1(其中$k=\frac{{y}_{M}+1}{{x}_{M}}$),联立直线方程和椭圆方程,求出Q坐标,得到AN、AQ的斜率,由kAN=kAQ,可得A、Q、N三点共线.
解答 (1)解:设E(t,t),则A(2t,2t+1),
∵点A在椭圆上,则$\frac{(2t)^{2}}{2}+(2t+1)^{2}=1$,解得t=$-\frac{2}{3}$或t=0(舍),
∴E($-\frac{2}{3},-\frac{2}{3}$),故直线AB的方程为$\frac{y+1}{-\frac{2}{3}+1}=\frac{x}{-\frac{2}{3}}$,
整理得:x+2y+2=0;
(2)证明:①设P(x0,y0),则$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}=1$,
直线AP:$y+\frac{1}{3}=\frac{{y}_{0}+\frac{1}{3}}{{x}_{0}+\frac{4}{3}}(x+\frac{4}{3})$,与直线y=x联立得:${x}_{M}=\frac{4{y}_{0}-{x}_{0}}{3({x}_{0}-{y}_{0}+1)}$;
直线BP:$y+1=\frac{{y}_{0}+1}{{x}_{0}}x$,与直线y=x联立得:${x}_{N}=\frac{-{x}_{0}}{{x}_{0}-{y}_{0}-1}$.
∴|OM||ON|=$\sqrt{2}|{x}_{M}|•\sqrt{2}|{x}_{N}|=2$$|\frac{4{y}_{0}-{x}_{0}}{3({x}_{0}-{y}_{0}+1)}|•|\frac{-{x}_{0}}{{x}_{0}-{y}_{0}-1}|$=$\frac{2}{3}|\frac{{{x}_{0}}^{2}-4{x}_{0}{y}_{0}}{({x}_{0}-{y}_{0})^{2}-1}|$
=$\frac{2}{3}|\frac{{{x}_{0}}^{2}-4{x}_{0}{y}_{0}}{{{x}_{0}}^{2}+{{y}_{0}}^{2}-2{x}_{0}{y}_{0}-1}|$=$\frac{2}{3}|\frac{{{x}_{0}}^{2}-4{x}_{0}{y}_{0}}{{{x}_{0}}^{2}+1-\frac{{{x}_{0}}^{2}}{2}-2{x}_{0}{y}_{0}-1}|$=$\frac{2}{3}|\frac{{{x}_{0}}^{2}-4{x}_{0}{y}_{0}}{\frac{{{x}_{0}}^{2}}{2}-2{x}_{0}{y}_{0}}|=\frac{4}{3}$为定值;
②设直线BM:y=kx-1(其中$k=\frac{{y}_{M}+1}{{x}_{M}}$),
联立$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,得(1+2k2)x2-4kx=0,
∴${x}_{Q}=\frac{4k}{1+2{k}^{2}},{y}_{Q}=\frac{2{k}^{2}-1}{1+2{k}^{2}}$,
${k}_{AN}=\frac{{y}_{N}+\frac{1}{3}}{{x}_{N}+\frac{4}{3}}=\frac{3{y}_{N}+1}{3{x}_{N}+4}$=$1-\frac{3}{3{x}_{N}+4}$,
${k}_{AQ}=\frac{{y}_{Q}+\frac{1}{3}}{{x}_{Q}+\frac{4}{3}}=\frac{2k-1}{2k+2}=1-\frac{3}{2(k+1)}$.
要证A、Q、N三点共线,只要证kAN=kAQ,只需证:3xN+4=2k+2,
把k=$\frac{{y}_{M}+1}{{x}_{M}}$代入,即证${x}_{M}•{x}_{N}=\frac{2}{3}$.
由①的证明过程知|xM|•|xN|=$\frac{2}{3}$,而xM,xN同号,
∴${x}_{M}•{x}_{N}=\frac{2}{3}$.
即A、Q、N三点共线.
点评 本题考查直线与圆锥曲线位置关系的应用,考查学生的逻辑思维能力和运算求解能力,体现了整体运算思想方法,综合性强,难度较大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 直线m,n和平面α成等角 | B. | m⊥α且n⊥α | ||
| C. | m∥α且n?α | D. | m∥α且n∥α |

| A. | k≤3 | B. | k≤4 | C. | k≤5 | D. | k≤6 |
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
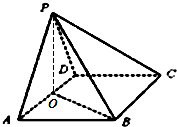 如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.