题目内容
设函数
（Ⅰ）若f（x）在x=2时有极值，求实数a的值和f（x）的单调区间；
（Ⅱ）若f（x）在定义域上是增函数，求实数a的取值范围．
（Ⅰ）若f（x）在x=2时有极值，求实数a的值和f（x）的单调区间；
（Ⅱ）若f（x）在定义域上是增函数，求实数a的取值范围．
解：（1）∵f（x）在x=2时有极值，
∴有f'（2）=0，
又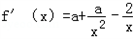
，
∴有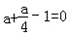
，∴
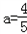
∴有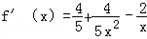
=
，
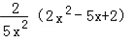由f'（x）=0有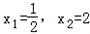
，
将x，f'（x），f（x）关系列表如下，定义域为（0，+∞）
（Ⅱ）若f（x）在定义域上是增函数，则f'（x）≥0在x＞0时恒成立，
∵
，
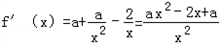∴需x＞0时ax2﹣2x+a≥0恒成立，化为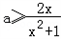
恒成立，
∵
，
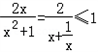∴a≥1，此为所求
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
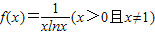
对任意x∈（0，1）成立，求实数a的取值范围．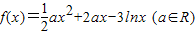
，