题目内容
11.在直角坐标系xoy中,圆C1:x2+y2=4,圆C2:(x-2)2+y2=4.(1)求圆C1与C2的公共弦所在直线方程;
(2)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1、C2的极坐标方程,并求出圆C1、C2的交点的极坐标.
分析 ((1)两圆方程相减求出公共弦所在直线的解析式;
(2)根据极坐标与直角坐标互化的公式,分别算出两圆的极坐标方程;再根据两圆的位置关系,可得它们的交点距离原点的距离和射线与x轴正半轴所成的角,即可得到两圆交点的极坐标.
解答 解:(1)圆C1:x2+y2=4,圆C2:(x-2)2+y2=4,
方程相减得圆C1与圆C2的公共弦所在直线的方程:x=1;
(2)解圆C1:x2+y2=4,化成极坐标方程为ρ2=4,解之得ρ=2
∵圆C2:(x-2)2+y2=4,展开得x2+y2-4x=0,
∴⊙C2化成极坐标方程为ρ2-4ρcosθ=0,化简得ρ=4cosθ
又∵⊙C1与⊙C2在直角坐标下交于点A(1,$\sqrt{3}$),B(2,-$\sqrt{3}$)
∴点A的极径ρ1=2,极角θ1=$\frac{π}{3}$,得A的极坐标为(2,$\frac{π}{3}$)
同理,得A的极坐标为(2,-$\frac{π}{3}$).
点评 此题考查了直线与圆相交的性质,考查了极坐标与直角坐标互化的公式、直线与圆的位置关系等知识点,求出公共弦所在的直线方程是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.复数${m^2}-2m+\frac{{{m^2}+m-6}}{m}i$为纯虚数,则实数m的值为( )
| A. | m≠2且m≠3 | B. | m≠2,m≠3且m≠0 | C. | m=3 | D. | 不存在 |
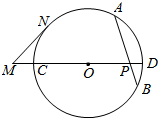 如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.
如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.