题目内容
2．已知奇函数y=f（x）定义域是R，当x≥0时，f（x）=x（1-x）．（1）求出函数y=f（x）的解析式；
（2）写出函数y=f（x）的单调递增区间．（不用证明，只需直接写出递增区间即可）
分析 （1）当x＜0时，-x＞0，根据已知可求得f（-x），根据奇函数的性质f（x）=-f（-x）即可求得f（x）的表达式．
（2）结合二次函数的图象和性质，可得分段函数的单调递增区间．
解答 解：（1）当x＜0时，-x＞0，
∴f（-x）=-x（1+x）．…（3分）
又因为y=f（x）是奇函数
所以f（x）=-f（-x）x（1+x）．…（6分）
综上f（x）=$\left\{\begin{array}{l}x（1-x），x≥0\\ x（1+x），x＜0\end{array}\right.$…（8分）
（2）函数y=f（x）的单调递增区间是[$-\frac{1}{2}$，$\frac{1}{2}$]…（12分）
点评 本题考查的知识点是函数奇偶性的性质，难度不大，属于基础题．
练习册系列答案
相关题目
13．
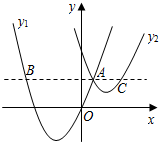如图，抛物线y1=a（x+2）2-3与y2=$\frac{1}{2}$（x-3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：
①无论x取何值，y2的值总是正数；
②a=1；
③当x=0时，y2-y1=4；
④2AB=3AC．
其中正确结论是（ ）
如图，抛物线y1=a（x+2）2-3与y2=$\frac{1}{2}$（x-3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：①无论x取何值，y2的值总是正数；
②a=1；
③当x=0时，y2-y1=4；
④2AB=3AC．
其中正确结论是（ ）
| A． | ①② | B． | ②③ | C． | ③④ | D． | ①④ |
10．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（φ＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入了部分数据，如下表：
（Ⅰ）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数f（x）的解析式；
（Ⅱ）将y=f（x）图象上所有点向右平行移动$\frac{π}{3}$个单位长度，得到y=g（x）图象，求y=g（x）的图象离y轴最近的对称轴．
| φx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | ||
| Asin（φx+φ） | 0 | 3 | 0 | -3 | 0 |
（Ⅱ）将y=f（x）图象上所有点向右平行移动$\frac{π}{3}$个单位长度，得到y=g（x）图象，求y=g（x）的图象离y轴最近的对称轴．
17．各顶点都在一个球面上的正四棱柱的高是2，体积是16，则这个球的表面积是（ ）
| A． | 16π | B． | 20π | C． | 24π | D． | 32π |