题目内容
1.已知椭圆x2+2y2=8的两个焦点分别为F1、F2,A为椭圆上任意一点,AP是△AF1F2的外角平分线,且$\overrightarrow{AP}•\overrightarrow{{F_2}P}$=0,则点P的轨迹方程为x2+y2=8.分析 根据等腰三角形“三线合一”,得到|MP|=|F2P|,从而|PF1|+|PF2|=|MF1|,结合椭圆的定义可得|MF1|=2a,运用中位线定理,即可得到动点P的轨迹对应的图形.
解答 解:椭圆x2+2y2=8,即为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1,
可得a=2$\sqrt{2}$,
$\overrightarrow{AP}•\overrightarrow{{F_2}P}$=0,可得$\overrightarrow{AP}$⊥$\overrightarrow{{F}_{2}P}$,
延长F1A和F2P交于M,连接OP,
可得|MP|=|F2P|,即有|PF1|+|PF2|=|AM|+|AF2|=|MF1|,
根据椭圆的定义,可得|PF1|+|PF2|=4$\sqrt{2}$,
∴|MF1|=4$\sqrt{2}$,
由中位线定理可得|OP|=$\frac{1}{2}$|MF1|=2$\sqrt{2}$,
因此,点P的轨迹是以点O为圆心,半径为2$\sqrt{2}$的圆x2+y2=8.
故答案为:x2+y2=8.
点评 本题给出椭圆上动点A,求点P的轨迹方程,着重考查了椭圆的定义和简单几何性质,以及等腰三角形“三线合一”等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知f(x)=sinnx,则f′(x)=( )
| A. | nsinn-1x | B. | ncosn-1x | C. | cosnx | D. | nsinn-1x•cosx |
9.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)<x,则不等式(x+1)2f(x+1)-4f(-2)>0的解集为( )
| A. | (-∞,-2) | B. | (-2,-1) | C. | (-∞,-3) | D. | (-3,-1) |
 在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.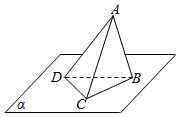 如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.
如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.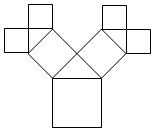 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.