题目内容
 如图,已知PA与圆O相切于A,半径OC⊥OP,AC交PO于B,若OC=1,OP=2,则PA=________,PB=________.
如图,已知PA与圆O相切于A,半径OC⊥OP,AC交PO于B,若OC=1,OP=2,则PA=________,PB=________.


分析:由切割线定理可得PA2=PE•PF,即可得出PA,再根据圆的切线的性质、互余角的关系及对顶角即可得出∠PAB=∠ABP,从而求出PB.
解答:设OP与⊙O相较于点E,并延长PO交⊙O于点F,由PA与圆O相切于A,

根据切割线定理可得PA2=PE•PF,∴PA2=(2-1)×(2+1),解得PA=
 .
.连接OA,则∠PAO=90°,
∵∠OAB+∠PAB=90°,∠OBC+∠OCA=90°,
∠OAC=∠OCB,∠ABP=∠OBC,
∴∠PAB=∠ABP.
∴PB=PA=
 .
.故答案分别为
 ,
, .
.点评:熟练掌握切割线定理、圆的切线的性质、互余角的关系及对顶角的性质是解题的关键.

练习册系列答案
相关题目
 (几何证明选讲选做题)
(几何证明选讲选做题)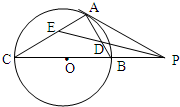 (2012•太原模拟)选修4-1:几何证明选讲
(2012•太原模拟)选修4-1:几何证明选讲 选修4-1:几何证明选讲
选修4-1:几何证明选讲 如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO点C,若圆O的半径为3,OP=5,则BC的长度
如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO点C,若圆O的半径为3,OP=5,则BC的长度 选修4-1:几何证明选讲
选修4-1:几何证明选讲