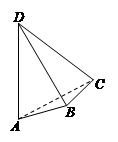题目内容
设P是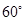 的二面角
的二面角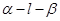 内一点,
内一点,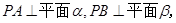
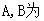 垂足,
垂足,
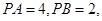 则AB的长为( )
则AB的长为( )
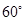 的二面角
的二面角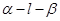 内一点,
内一点,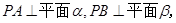
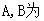 垂足,
垂足,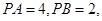 则AB的长为( )
则AB的长为( )A.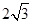 | B.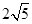 | C.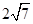 | D.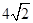 |
C
解:设平面PAB与二面角的棱l交于点Q,
连接AQ、BQ可得直线l⊥平面PAQB,
所以∠AQB是二面角α-l-β的平面角,∠AQB=60°,
故△PAB中,∠APB=180°-60°=120°,PA=4,PB=2,
由余弦定理得:AB2=PA2+PB2-2PA•PBcos120°,=42+22-2×4×2×(-1 2 ) =28,
2 ) =28,
所以AB=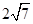 ,故选C.
,故选C.
连接AQ、BQ可得直线l⊥平面PAQB,
所以∠AQB是二面角α-l-β的平面角,∠AQB=60°,
故△PAB中,∠APB=180°-60°=120°,PA=4,PB=2,
由余弦定理得:AB2=PA2+PB2-2PA•PBcos120°,=42+22-2×4×2×(-1
 2 ) =28,
2 ) =28,所以AB=
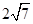 ,故选C.
,故选C.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
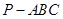 中,
中,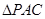 和
和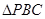 是边长为
是边长为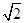 的等边三角形,
的等边三角形,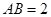 ,
,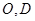 分别是
分别是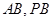 的中点.
的中点.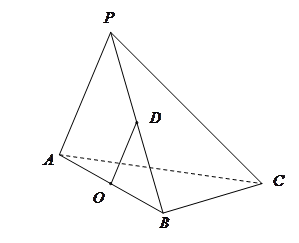
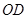 ∥平面
∥平面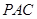 ;
;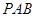 ⊥平面
⊥平面 ;
;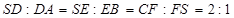 ,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )
,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )

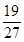
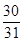
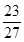
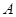 .
.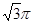
 .
.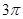
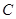 .
.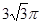
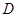 .
.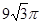
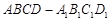 中,
中,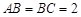 ,过
,过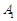 、
、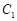 、
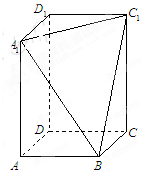
、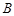 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体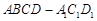 ,且这个几何体的体积为
,且这个几何体的体积为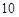 .
.
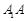 的长;
的长;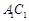 的中点为
的中点为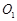 ,求异面直线
,求异面直线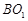 与
与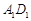 所成角的余弦值.
所成角的余弦值.