��Ŀ����
14����ֱ������ϵxOy�У�ԲC1��C2�IJ������̷ֱ���$\left\{\begin{array}{l}x=2+2cosϕ\\ y=2sinϕ\end{array}\right.$��ϕΪ��������$\left\{\begin{array}{l}x=cos��\\ y=1+sin��\end{array}\right.$����Ϊ����������OΪ���㣬x���������Ϊ���Ὠ��������ϵ����1����ԲC1��C2�ļ����귽�̣�
��2������OM����=����ԲC1�Ľ���ֱ�ΪO��P����ԲC2�Ľ���ֱ�ΪO��Q����|OP|•|OQ|�����ֵ��
���� ��1���ȷֱ������ͨ���̣���д�������귽�̣�
��2�����ü��������壬���ɵó����ۣ�
��� �⣺��1��ԲC1��C2�IJ������̷ֱ���$\left\{\begin{array}{l}x=2+2cosϕ\\ y=2sinϕ\end{array}\right.$��ϕΪ��������$\left\{\begin{array}{l}x=cos��\\ y=1+sin��\end{array}\right.$����Ϊ��������
��ͨ���̷ֱ�Ϊ��x-2��2+y2=4��x2+��y-1��2=1�������귽�̷ֱ�Ϊ��=4cos�ȣ���=2sin�ȣ�
��2����P��Q��Ӧ�ļ����ֱ�Ϊ��1����2����|OP|•|OQ|=��1��2=4sin2����
��sin2��=1��|OP|•|OQ|�����ֵΪ4��
���� ���⿼�����ַ��̵�ת�������鼫������������ã������е��⣮

��ϰ��ϵ�д�
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
�����Ŀ
4����֪$\overrightarrow{a}$��$\overrightarrow{b}$������������|$\overrightarrow{a}$|=1��|$\overrightarrow{b}$|=2���ң�$\overrightarrow{a}$+$\overrightarrow{b}$����$\overrightarrow{a}$�����ڡ�ABC�У�$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AC}$=$\overrightarrow{b}$��DΪBC�е㣬��AD�ij�Ϊ��������
| A�� | $\frac{{\sqrt{7}}}{2}$ | B�� | $\frac{{\sqrt{6}}}{2}$ | C�� | $\frac{{\sqrt{5}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
2��������y=$\frac{1}{4}$x2���߷����ǣ�������
| A�� | y=-1 | B�� | y=1 | C�� | x=-$\frac{1}{16}$ | D�� | x=$\frac{1}{16}$ |
9������C�IJ�������Ϊ$\left\{{\begin{array}{l}{x=4cos��}\\{y=sin��}\end{array}}\right.$����Ϊ��������M������C�ϵĶ��㣬������T�����귽��2��sin��+��cos��=20�����M��T�ľ�������ֵ��������
| A�� | $\sqrt{13}+4\sqrt{5}$ | B�� | $2+4\sqrt{5}$ | C�� | $4+4\sqrt{5}$ | D�� | $6\sqrt{5}$ |
 ������P-ABCE�У�PA�͵���ABCE��CD��AE��ACƽ�֡�BAD��GΪPC���е㣬PA=AD=2��BC=DE��AB=3��CD=2$\sqrt{3}$��F��M�ֱ�ΪBC��EG��һ�㣬��AF��CD��
������P-ABCE�У�PA�͵���ABCE��CD��AE��ACƽ�֡�BAD��GΪPC���е㣬PA=AD=2��BC=DE��AB=3��CD=2$\sqrt{3}$��F��M�ֱ�ΪBC��EG��һ�㣬��AF��CD��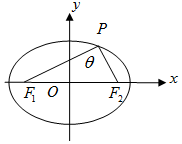 ��Բ$\frac{x^2}{4}+{y^2}$=1�ϵ�һ��P��������F1��F2�����ɵ������γ�Ϊ���������Σ�
��Բ$\frac{x^2}{4}+{y^2}$=1�ϵ�һ��P��������F1��F2�����ɵ������γ�Ϊ���������Σ�