题目内容
在双曲线
－
＝1的一支上有三个不同的点A(x1，y1)、B(
，6)、C(x2，y2)，它们与焦点F(0，5)的距离成等差数列，求y1＋y2的值．
答案：
解析：
解析：
|
解：由方程知a＝ ∴e＝ 由双曲线的第二定义知
∴｜AF｜＝ ∵A、B、C在双曲线同一支上，而B在上支上， ∴A、C也在双曲线的上支 ｜AF｜＝ 同理｜BF｜＝ ｜CF｜＝ ∴｜AF｜＋｜CF｜＝2｜BF｜． ∴y1＋y2＝12． 分析：将｜AF｜、｜BF｜、｜CF｜转化为A、B、C到相应准线的距离，可使问题获得解决． 点评：在问题中，当涉及到焦半径、焦点弦的问题时，常把点焦距转化为点到相应准线的距离． |
＝2
，b＝
，c＝5．
，上焦点F相应的准线为y＝
．
＝
练习册系列答案
阅读快车系列答案
相关题目
－
＝－1的一支上有不同的三点A(x1，y1)，B(x2，6)，C(x3，y3)，它们与焦点F(0，5)的距离成等差数列．
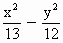＝－1的一支上有不同三点A
，6)，C(
)与焦点F(0，5)的距离成等差数列，(1)求
；(2)求证线段AC的垂直平分线经过某一定点，并求出定点的坐标．